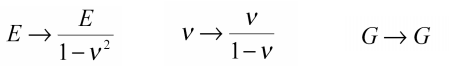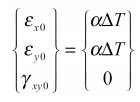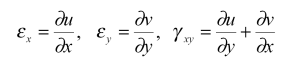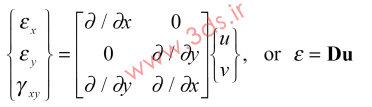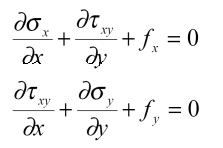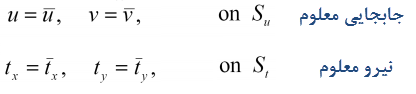پس از آشنایی با نحوه استخراج ماتریس سختی در المانهای میله، تیر و قاب در حالت کلی (اینجا: ماتریس سختی المان Bar دوبعدی، استخراج ماتریس سختی المان Beam)، ضروری است تا اصول اولیه حاکم بر مسائل مکانیک جامدات در حوزه اجزای محدود را فراگیریم. از اینرو در آموزش پیشرو قصد داریم تا شما همراهان گرامی را با مفاهیم ضروری در مسائل مکانیک جامدات دوبعدی آشنا کنیم. پیشنهاد میکنم قبل از شروع بحث، در ذهن خود مروری بر مفاهیم اولیه مقاومت مصالح در زمینه تانسورهای تنش و کرنش و مسائل تنش / کرنش صفحهای داشته باشید (مسائل تنش صفحهای، کرنش صفحهای و تقارن محوری چیست؟). ما را در آموزش اجزا محدود “مسائل جامدات دوبعدی” همراهی کنید.
مروری بر تئوری پایه جامدات
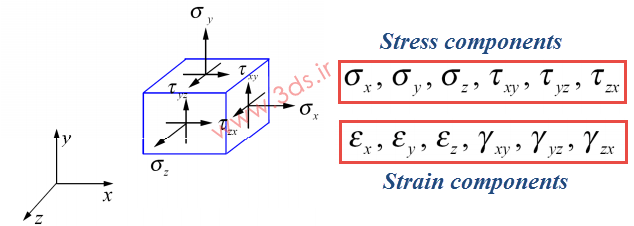
چنانچه به خاطر داشته باشید، در حالت کلی بارگذاری هر المان دارای شش مؤلفه تنش و کرنش مطابق تصویر زیر است:
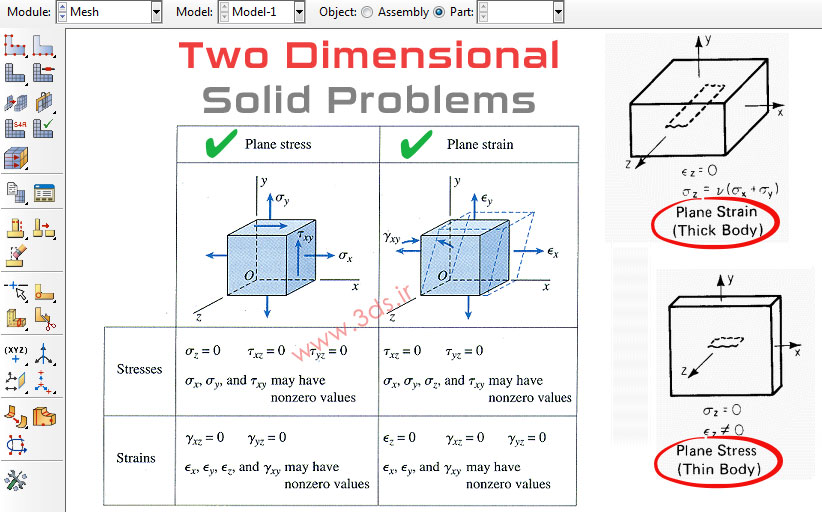
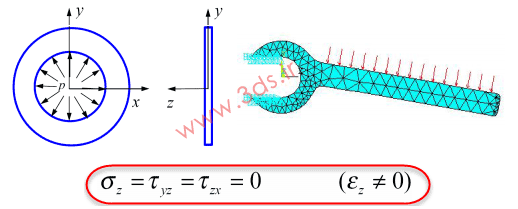
اما در شرایطی خاص و برای حالاتی از تنش و کرنش، میتوان مسائل جامدات را با سادهسازی از حالت سهبعدی به حالت دو بعدی تبدیل نمود. بعنوان مثال، برای سازههای صفحهای با ضخامت کم و ثابت، اگر بارگذاری در همان صفحه xy صورت گیرد، مسئله را به صورت تنش صفحهای در نظر میگیریم و مطابق زیر، قادر به حذف مؤلفههایی از تنش را خواهیم بود:
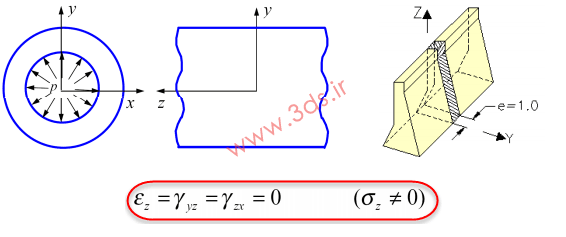
همچنین، برای سازههایی با ضخامت زیاد و سطح مقطع یکنواخت؛ در صورتی که بارگذاری در راستای ضخامت (راستای Z) صورت گیرد مسئله تبدیل به حالت کرنش صفحهای شده و مؤلفههایی از تنش حذف خواهد شد:
روابط اجزای محدودی حاکم
با توجه به معادلات اشاره شده در بخش پیشین، میتوان معادلات تنش-کرنش حاکم بر مسائل تنش صفحهای را به صورت زیر استخراج کرد:
در حالت کرنش صفحهای کافیست مقادیر ثابت موجود در معادلات فوق را با مقادیر زیر جایگزین نماییم:
در نتیجه :
که در آن، کرنشهای اولیه به واسطه تغییرات درجه حرارت برابر است با:
حال، برای مقادیر کوچک کرنش و دوران میتوان نوشت:
و یا در فرم ماتریسی:
معادلات تعادل و شرایط مرزی
حال که با روابط فوق آشنا شدهاید، خالی از لطف نیست که مروری گذرا بر معادلات تعادل داشته باشیم. همانطور که از تئوری الاستیسیته بخاطر دارید، تنش در یک سازه باید در معادلات تعادل صدق نماید:
که در آن fx و fy معرف نیروهای حجمی (مانند مغناطیس یا وزن) هستند. فراموش نکنید در روش اجزای محدود، معادلات تعادل به صورت تقریبی برقرار میشوند.
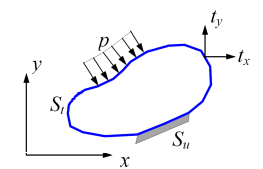
همچنین مطابق تصویر زیر، مرز S از یک سازه میتواند به دو قسمت تقسیم گردد:
که شرایط مرزی روی هر یک از این دو بخش به صورت زیر خواهد بود:
به عبارت دیگر در یک بخش از مرز موردنظر مقادیر جابجایی و در بخش دیگر مؤلفههای بارگذاری به صورت مقادیر معلوم وارد حل مسئله میشوند. در روش اجزا محدود، انواع بارگذاری نظیر بارهای گسترده بر روی سطوح، بارگذاریهای حجمی، نیروهای متمرکز و گشتاورها به صورت نیروهای نقطهای در گرهها تبدیل خواهند شد.
بهعنوان نکته پایانی بخاطر داشته باشید برای حل دقیق (تغییر مکان، کرنش و تنش) یک سازه باید معادلات تعادل برقرار گردند و در کنار آن، شرایط مرزی و شرایط سازگاری مسئله (میدان تغییر مکان سازه باید بهصورت پیوسته تغییر نماید و دارای گسستگی و همپوشانی نباشد) را نیز ارضا کنند.
منبع : آکادمی نرمافزارهای مکانیک