الزامات تولید توابع شکل در اجزا محدود

اهداف آموزش: در این آموزش با اصول اجزا محدود حاکم بر حل یک مسئله آشنا خواهید شد. همچنین با معرفی و شناخت توابع شکل، پل میان محاسبات گره‌ای و محاسبات داخل المان را برقرار خواهیم کرد. شناخت الزامات و چارچوب‌های توابع شکل در اجزا محدود از دیگر اهدافی است که با مطالعه این آموزش به آن خواهید رسید.

نقش تابع شکل در اجزا محدود

پیش‌تر و در سلسله آموزش‌های روش اجزا محدود به معرفی نقش و جایگاه توابع شکل و المان‌ها در آباکوس پرداختیم. اگر مبانی مربوط به علم اجزا محدود را به‌درستی فرا گرفته باشید می‌دانید که اساس این روش، بر محاسبه مقادیر موردنظر در گره‌های هر المان استوار است. محاسبات مربوطه در گره‌ها انجام می‌شود و سپس به هر نقطه دلخواه از المان پیوند داده می‌شود. توابع شکل نقش این رابط‌های محاسباتی را بر عهده دارند. به شکل خلاصه، توابع شکل را باید مجموعه توابع میانیابی دانست که به کمک آن قادر خواهیم بود مقادیر محاسبه شده برای یک میدان متغیر در گره‌ها را به هر نقطه دلخواه از المان ارتباط دهیم.

برای استخراج و تولید توابع شکل، روش‌های گوناگونی نظیر چندجمله‌ای‌های لاگرانژ، روش مستقیم، توابع هرمیتی، اصول بر هم نهی، روش آیرون و حاصلضرب خطوط وجود دارد که هر یک دارای ویژگی‌ها و نقاط ضعف و قوت خاصی است که معرفی و بررسی آن از حوصله این بحث خارج است. اما تمامی روش‌های محاسباتی و استخراج فوق باید مجموعه الزامات و چارچوب‌های اجزا محدود را برآورده سازد.

در واقع محدوده میدان بازی و هدف توسط اجزا محدود تعیین شده و این شما هستید که فراخور دانش و تخصص خود یک روش بازی را انتخاب می‌کنید؛ روش بازی که قوانین حاکم را نقض نمی‌کند. بدون شک استفاده از یک وسیله یا ابزار بدون شناخت الزامات استفاده از آن لطفی ندارد، لذا در این آموزش اجزا محدود، قصد داریم تا شما همراهان گرامی را با الزامات تولید و استخراج توابع شکل آشنا کنیم. در این آموزش، چارچوب‌ها و قوانین حاکم بر تولید توابع شکل به هر روش دلخواه را مرور خواهیم کرد. با ما همراه باشید.

اصول اساسی اجزا محدود

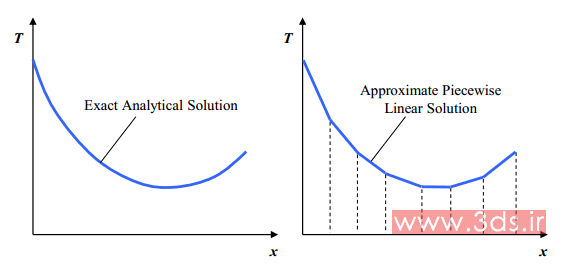
حتماً شما همراهان گرامی به این موضوع واقف هستید که هر حل میدان پیوسته نظیر تنش، جابجایی، دما، فشار و . . . در اجزا محدود، می‌تواند با یک مدل گسسته از مجموعه محدودی توابع تکه‌ای پیوسته، تقریب زده شود. برای درک بهتر موضوع، به تصویر زیر توجه کنید:

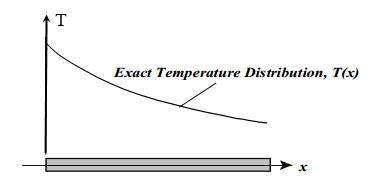
تصویر بالا، توزیع دمای یک بعدی در یک نمونه فرضی را نشان می‌دهد. نمودار سمت چپ، مربوط به حل دقیق و در اصطلاح تحلیلی مسئله است و نمودار سمت راست، حل تقریبی همان مسئله به کمک توابع تکه‌ای پیوسته خطی را به تصویر کشیده است. اجازه دهید نگاهی نزدیک‌تر به همین مسئله داشته باشیم و اصول اجزا محدود را در قالب همین مثال ساده پیش ببریم.

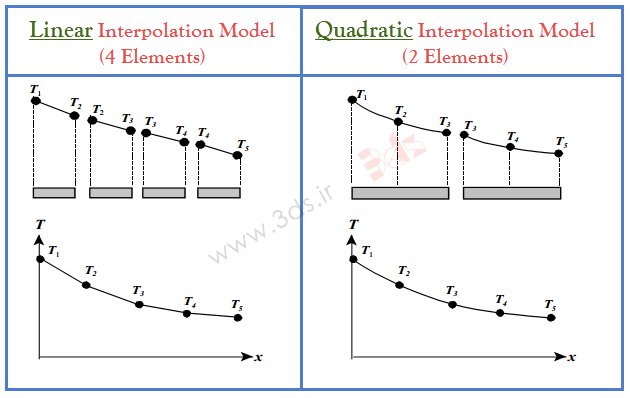
فرض کنید قصد داریم، قطعه‌ای که نمودار توزیع دمای آن‌را مشاهده کردیم، به مجموعه قطعات کوچکتر تقسیم کنیم. بدیهی است در این حالت، نمودار مربوط به توزیع دمای کل قطعه، به مجموعه توابع کوچکتر برای هر بخش تجزیه خواهد شد. بسته به اینکه قصد دارید در تقریب دمای هر بخش از قطعه اصلی، از چه تابعی استفاده کنید، پاسخ مسئله متفاوت خواهد بود. در ستون سمت چپ از تصویر زیر، از یک مدل درونیاب خطی برای تقریب توزیع دما در نمونه استفاده شده است، در حالی که ستون سمت راست، حل همین مسئله به‌وسیله توابع درونیاب مرتبه دوم را نشان می‌دهد.

در واقع تصویر سمت چپ، تقریب تکه‌ای خطی را نشان می‌دهد که در آن میدان دمایی پیوسته اما گرادیان دما ناپیوسته است؛ در حالی‌که در تصویر سمت راست تقریب تکه‌ای درجه دو نشان داده شده که میدان دما و گرادیان دما در آن پیوسته هستند.

نقاط مشترک توابع تقریب

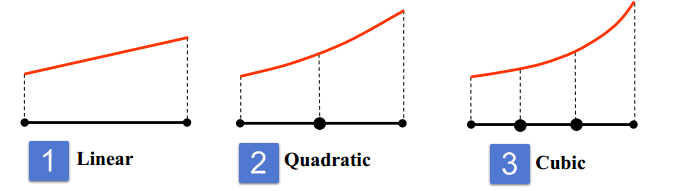
در بیشتر مواقع، از چندجمله‌ای‌ها برای توابع تقریب در هر المان استفاده می‌شود. بسته به مرتبه تقریب، تعداد متفاوتی از پارامترهای هر المان برای ایجاد کردن توابع تقریب مورد نیاز است.

اما برای برخی مسائل (مانند المان‌های نیمه بی‌نهایت، مدل‌سازی ترک و سایر المان‌های تکین یا منفرد) توابع تقریب به نحوی انتخاب شوند تا علاوه بر برآورده کردن الزامت و قیود حاکم بر اجزا محدود، خواص ویژه‌ای را که در بررسی‌های تئوری این مسائل وجود دارد نیز پوشش دهند. در ادامه این آموزش، به بررسی قواعد و اصولل حاکم بر استخراج توابع شکل خواهیم پرداخت.

الزامات توابع شکل

به‌عنوان اولین و ساده‌ترین اصل،  توابع شکل باید شرایط همگرایی حل را ارضا نمایند؛ به‌عبارت بهتر با بهبود سایز شبکه و یافتن تعداد المان‌های مناسب، حل اجزا محدود مسئله باید به حل تحلیلی آن نزدیک شود. در همین راستا:

• الزامات سازگاری مسئله (Compatibility)

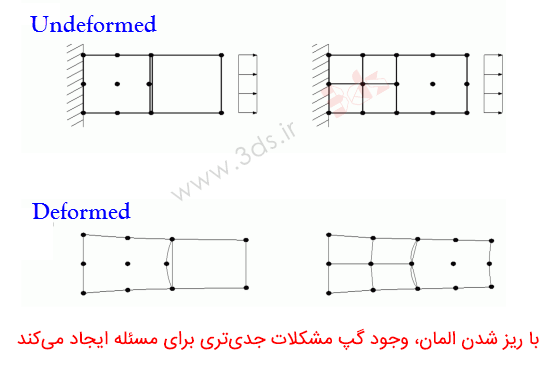
توابع درونیاب باید به گونه‌ای انتخاب شوند که میدان جابجایی مسئله در داخل هر المان پیوسته و مشتق‌پذیر باشد. همچنین میدان جابجایی مورد نظر باید در مرزهای المان دارای پیوستگی باشد. المان‌هایی که شرط فوق را برآورده می‌کنند به المان‌های سازگار یا Compatible معروف هستند (و المان‌هایی که شرایط فوق را نقض کنند،، Incompatible نامیده می شوند). توابع شکل باید شرط پیوستگی جابجایی بین المان‌ها را ارضا کنند. از نقطه نظر فیزیکی، این قید تضمین می‌کند تا با تغییر شکلل المان‌ها، تخلخل یا گپی در بین المان‌ها ایجاد نشود. وچود گپ‌ها هنگامی که از تعداد المان‌های بیشتری در حل استفاده می‌کنید جدی‌تر شده و می‌تواند مشکلات اساسی از نقطه نظر انرژی در مسئله پدید آورد. شکل زیر بحرانی شدن وضعیت، با ریز شدن المان‌ها را به تصویر کشیده است.

• الزامات تکامل (Completeness)

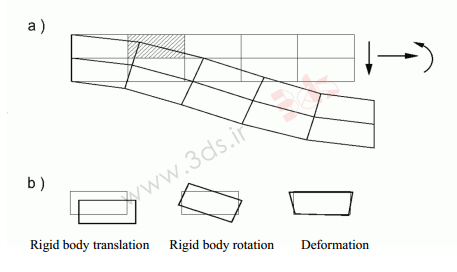
توابع درونیاب باید بتوانند حرکت جسم صلب را پوشش داده و حالت کرنش ثابت را مدل‌سازی کنند.

حال اگر بخواهیم موارد فوق را به زبان ریاضی شرح دهیم باید بگوییم چنانچه تابع زیر انتگرال در ماتریس سختی، از مرتبه m مشتق‌پذیر باشد، الزامات توابع شکل به صورت زیر تعریف خواهد شد:

• توابع شکل باید در بین المان‌ها دارای پیوستگی از مرتبه m-1 و در داخل هر المان مشتق‌پذیر از مرتبه m باشند (شرط پیوستگی).
• توابع شکل المان‌ها باید به شکل دقیق تمامی جمله‌های از مرتبه کوچکتر m را در چندجمله‌ای خود داشته باشند (در مختصات کارتزین)؛ مجموعه توابع شکلی که این شرط را ارضا نماید m-complete نامیده می‌شوند (شرط تکامل).

خواص توابع شکل

به شکل کلی توابع شکل با هر روشی که ایجاد شده باشند، خواص زیر را پوشش خواهند داد:

1. خاصیت دلتای کرانیکر: تابع شکل مربوط به هر گره مقداری برابر با 1 در همان گره دارد و در تمامی گره‌های دیگر برابر صفر است.
2. سازگاری: تقریب جابجایی باید در مرزهای المان‌ها پیوستگی داشته باشد.
3. تکامل: باید شرایط حرکت جسم صلب و همچنین حالت تنش ثابت ارضا شود.

به عنوان نکته پایانی فراموش نکنید ترکیب سازگاری و تکامل، همگرایی حل را نتیجه خواهد داد. در مجموعه پست‌های آینده به معرفی توابع درونیاب لاگرانژ خواهیم پرداخت. آموزش‌های اجزا محدود ما را دنبال کنید . . .

منبع: آکادمی نرم‌افزارهای مکانیک