المان‌های Incompatible Mode آباکوس

اهداف آموزش: با مطالعه این آموزش شناخت کافی از المان‌های Incompatible mode در آباکوس پیدا خواهید کرد. همچنین نقاط ضعف و قوت المان‌های Incompatible mode را فراخواهید گرفت. معرفی درجات آزادی المان‌های Incompatible mode در آباکوس؛ مقایسه المان‌‌های Incompatible mode و المان‌های درجه دو نیز مباحث آخر این آموزش است.

در مجموعه مطالب آموزشی پیشین در خصوص المان‌ها (المان‌های Shell یا پوسته‌ای، المان‌های Full Integration ، المان‌های Reduced Integration آباکوس) و مشکلات برخی از این المان‌ها (پدیده Shear Locking یا قفل‌شدگی برشی در آباکوس، پدیده Hourglass یا ساعت شنی در آباکوس)؛ سعی کردیم اطلاعات شما همراهان گرامی در خصوص انواع المان‌های موجود در نرم‌افزارهای اجزا محدود و مشکلات استفاده از آن‌ها افزایش یابد. جالب اینجاست که دانسته‌هایتان در این زمینه تنها به نرم‌افزار Abaqus  محدود نبوده و در نرم‌افزارهای رایجی نظیر انسیس (ANSYS) و نسترن (Nastran) نیز قابل استفاده است. خوشحالیم که در این موضوع توانسته‌ایم گام‌های علمی مناسبی برداریم و در این آموزش آباکوس قصد داریم کار خود را تکمیل کنیم. المان‌های Incompatible تنها گروهی از المان‌ها هستند که تا کنون به آن نپرداخته‌ایم. پس مثل همیشه ما را در این آموزش همراهی کنید.

چرا المان Incompatible Mode ؟

یکی از راهکارها در خصوص رفع مشکل قفل‌شدگی برشی (Shear locking) در المان‌های خطی Full integration استفاده از المان های کاهش یافته (Reduced integration)  در آباکوس بود که به تفصیل به نقاط ضعف و روش رفع آن پرداختیم. ادامه تلاش‌ها برای رفع این مشکل، سبب پدید آمدن المان‌های Incompatible در نرم‌افزارهای اجزا محدود گردید. از آنجایی که این موضوع ناشی از عدم توانایی میدان جابجایی المان در مدل‌سازی سینماتیک خمش است، در Incompatible Elements درجات آزادی اضافه که گرادیان تغییر شکل المان را افزایش می‌دهند، به المان‌های مرتبه اول الحاق می گردند. این افزایش گرادیان موجب می شود که المان مرتبه اول بتواند تغییرات خطی گرادیان تغییر شکل را در فضای المان پوشش دهد (شکل سمت چپ). شکل استاندارد فرمول‌بندی المان، گرادیان ثابت تغییر شکل را در المان به همراه خواهد داشت (شکل سمت راست).

این افزایش گرادیان تغییر شکل در یک المان، پدیده‌ای داخلی است و به گره‌های آن تعمیم پیدا نمی‌کند.

نقاط ضعف و قوت المان‌های Incompatible Mode در آباکوس

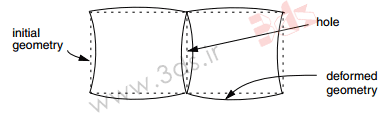بر خلاف فرمول‌بندی حالت Incompatible که میدان جابجایی را به شکل مستقیم ارتقا می‌دهد، فرمول‌بندی مورد استفاده در Abaqus سبب ایجاد فصل مشترک و یا حفره در مرز دو المان نمی‌شود. بنابراین، فرمول‌بندی مورد استفاده در Abaqus به‌راحتی قابل تعمیم به مسائل غیرخطی و تغییر شکل‌های کوچک است که خود یک نقطه قوت نسبت به روش فرمول‌بندی مستقیم به حساب می‌آید.

المان‌های مود Incompatible در مسائل خمش، منجر به نتایجی می‌شوند که قابل مقایسه با نتایج حاصل از المان‌های مرتبه دو می‌باشند با این تفاوت که زمان حل در المان‌های Incompatible کمتر بوده و کفه ترازو به سود آن‌هاست. فراموش نکنید که این المان‌ها با وجود پایین آوردن زمان حل، به اعوجاج حساس هستند. لذا در هنگام استفاده در مدل‌سازی هندسه‌های پیچیده که معمولا اعوجاج زیاد است استفاده از المان‌های مرتبه دوم Reduced Integration گزینه بهتری است زیرا به مراتب حساسیت کمتری نسبت به اعوجاج دارند.

منبع: آکادمی نرم‌افزارهای مکانیک