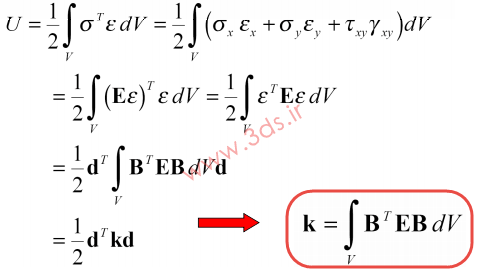اگر مجموعه آموزشهای اجزا محدود در آکادمی نرمافزارهای مکانیک را دنبال کرده باشید، با اصول حاکم بر حل یک مسئله به روش اجزا محدود، انتخاب المانها، مفهوم تابع شکل و المان میله در حالت دو و سهبعدی آشنا شدهاید. همچنین، اصول حاکم بر مسائل مکانیک جامدات از دیدگاه اجزا محدود آموختید (اینجا: مسائل جامدات دوبعدی : مفاهیم پایه). در این آموزش، قصد داریم تا شما را با روش اجزای محدود در مسائل دو بعدی آشنا کنیم. با ما همراه باشید.
لزوم استفاده از روش اجزا محدود در حل مسائل
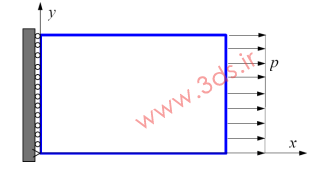
حتما شما همراهان گرامی به خوبی با این موضوع آشنا شدهاید که روش اجزا محدود، یک روش عددی برای حل معادلات دیفرانسیل حاکم بر یک مسئله واقعی است که در قالب یک مدل ریاضی آورده شده است. اگر به دروس پایه مکانیک نظیر الاستیسیته رجوع کنید به یاد میآورید که برای رسیدن به حل دقیق (تغییر مکان، کرنش و تنش) یک سازه، باید معادلات تعادل برقرار گردند و در کنار آن، شرایط مرزی و سازگاری مسئله نیز ارضا شوند (یادآوری: شرایط سازگاری بدین معناست که میدان تغییر مکان سازه باید به صورت پیوسته تغییر نماید و دارای گسستگی و همپوشانی نباشد). بدون شک حل معادلات تعادل در کنار برقراری شرایط مرزی و سازگاری در مسائل نه چندان پیچیده، کار سختی نیست؛ اما اگر با یک مسئله پیچیده (از نقطه نظر هندسه، رفتار ماده، بارگذاری و…) مواجه باشید، حل دقیق معادلات فوق عملاً بسیار دشوار و در برخی موادر تقریباً غیرممکن خواهد بود. برای مثال صفحه زیر را در نظر بگیرید که از یک سمت تحت بار کششی با مقدار مشخص قرار گرفته است.
حل دقیق مسئله فوق (یافتن مقادیر تغییر مکان، کرنش و تنش) در گرو حل دسته معادلات زیر خواهد بود.
اما حتما شما نیز با من موافقید که وجود یک حفره به شکل دایره یا مثلث در این صفحه، حل معادلات فوق را بسیار دشوار (و یا غیر ممکن) میسازد. لذا روش اجزای محدود در حل مسائل دوبعدی ابزاری بسیار گرهگشا خواهد بود.
روش اجزا محدود در مسائل دوبعدی
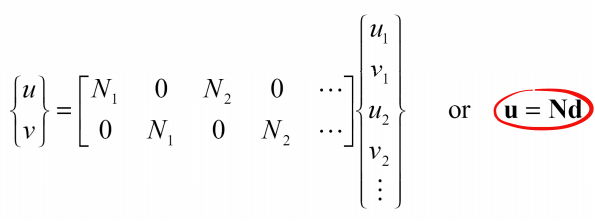
برای یک المان صفحهای، تغییر مکان (u,v) به صورت درونیابی از تغییر مکان گرهها (ui , vi) توسط توابع شکل، Ni بهدست میآید.
در رابطه فوق N، ماتریس تابع شکل، u بردار تغییر مکان و d بردار تغییر مکان گرهها است. با توجه به رابطه کرنش – تغییر مکان خواهیم داشت:
ماتریس B=DN، ماتریس کرنش- تغییر مکان نامیده میشود. از سوی دیگر، انرژی ذخیره شده در یک المان عبارت است از:
در این رابطه، K بیانگر ماتریس سختی است. برخلاف حالت یکبعدی، در اینجا E یک ماتریس است که از رابطه تنش – کرنش بهدست میآید (معادلات تنش صفحهای). با توجه به تقارن این ماتریس، K نیز یک ماتریس متقارن خواهد بود. برای یک ماده با خواص مشخص، ماتریس K بستگی کامل به ماتریس B و در نتیجه به توابع شکل دارد. بنابراین دقت روش اجزا محدود برای بررسی سازه به انتخاب توابع شکل برمیگردد. المانهای مورد استفاده در مسائل دوبعدی، المانهای مثلثی خطی و درجه دو، و المانهای مربعی خطی و درجه دو هستند. در ادامه مجموعه آموزش اجزا محدود شما را با المانهای مثلثی خطی آشنا خواهیم کرد.
اجزای محدود را حرفهای و دقیق بیاموزید …