اهداف آموزش: در این آموزش شما با مفاهیم الاستیسیته سهبعدی، نحوه پیادهسازی الاستیسیته سهبعدی در اجزا محدود، معادلات تعادل در الاستیسیته، استخراج روابط کرنش – جابجایی و نهایتا نحوه استخراج روابط تنش – کرنش در الاستیسیته آشنا خواهید شد.
اگر مجموعه آموزشهای اجزا محدود در سایت آکادمی نرمافزارهای مکانیک را دنبال کرده باشید، میدانید که در سلسله مباحث آموزشی این حوزه، به بحث و بررسی پیرامون استخراج ماتریس سختی در المانهایی مانند تیر و میله (ماتریس سختی المان تیر، ماتریس سختی المان میله)، آشنایی با توابع شکل در FEM و همچنین بسط و توسعه اجزاء محدود در مسائل دو بعدی پرداختیم. در این آموزش اجزا محدود قصد داریم تا شما را با مفاهیم الاستیسیته سهبعدی در اجزا محدود آشنا کنیم. پیشنهاد میکنم این آموزش کاربردی را مطالعه کنید.
مفاهیم پایه در الاستیسیته سهبعدی
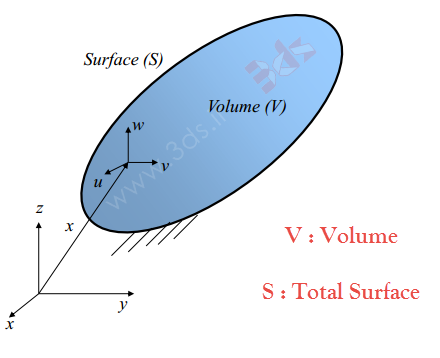
مطابق تصویر زیر جسمی سهبعدی با حجم V و مجموع سطوح S را در نظر بگیرید که تغییر شکل آن در نقطه [x,y,z] بوسیله سه مؤلفه جابجایی [u,v,w] توصیف میشود:
بر روی این جسم میتوان دو دسته نیروی خارجی اصلی اعمال کرد:
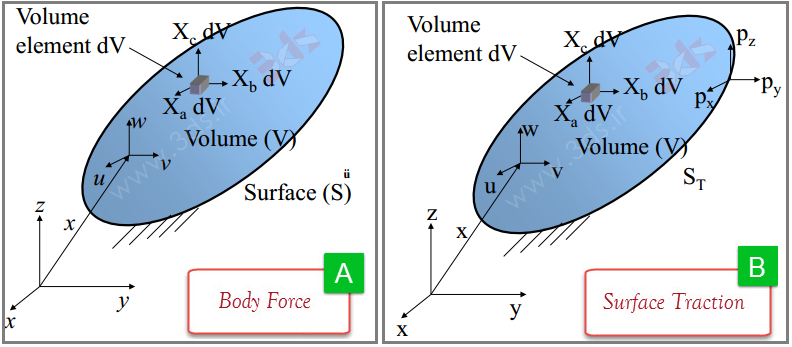
- نیروهای حجمی (Body Force): نیرو بر واحد حجم مانند وزن، اینرسی، الکترومغناطیس و . . .
- ترکشن سطحی (Surface Traction) : نیرو بر واحد سطح مانند اصطکاک.
در شکل سمت چپ اثر نیروهای حجمی و در شکل سمت راست اثر نیروهای ترکشن سطحی را مشاهده میکنید:
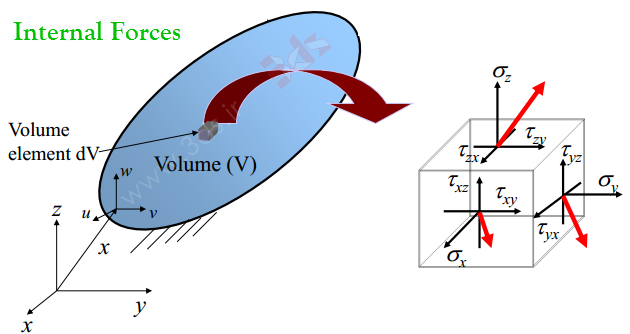
اگر یک تکه از ماده را از جسم اصلی جدا کنیم در مییابیم که بهدلیل نیروهای خارجی اعمال شده به آن، نیروهای عکسالعمل بر روی سطوح المان جدا شده وجود خواهد داشت (برای مثال در اثر نیروی اعمالی بر سازه یک خرپا، نیروهای داخلی در هر عضو سازه بوجود میآید).
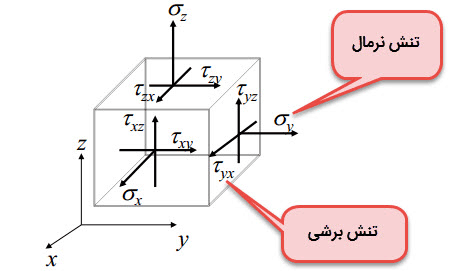
برای مکعب نشان داده شده در شکل بالا، نیروهای عکسالعمل داخلی بر واحد سطح (بردارهای قرمز رنگ) روی هر یک از وجوه، میتواند به سه مؤلفه متعامد تجزیه شود.
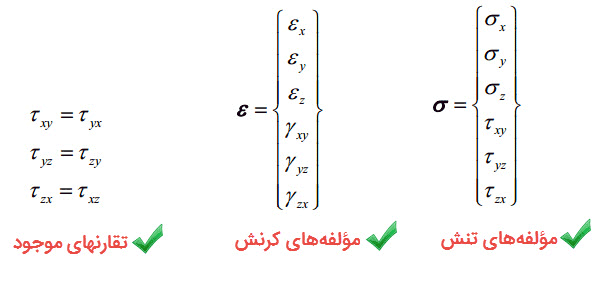
همانطور که از مقاومت مصالح به خاطر دارید، روی هر وجه از المان نشان داده شده، یک مؤلفه تنش نرمال و دو مؤلفه تنش برشی وجود خواهد داشت. از اینرو در مجموع 9 مؤلفه تنش خواهیم داشت که از بین آنها تنها 6 مؤلفه مستقل است.
با توجه به تئوریهای پایه الاستیسیته، 3 معادله تعادل الاستیسیته به شکل زیر خواهیم داشت:
در بررسی مسائل الاستیسیته سهبعدی نیاز داریم تا به درک روشن و کاملی از سه اصل زیر برسیم:
- درک معادلات دیفرانسیل حاکم به همراه شرایط مرزی (Strong Formulation)
- رابطه کرنش – جابجایی
- رابطه تنش – کرنش
در ادامه این آموزش، به بررسی موارد فوق میپردازیم.
معادلات دیفرانسیل حاکم به همراه شرایط مرزی
بر اساس فرمولبندی Strong یا در اصطلاح فرم قوی مسائل الاستیسیته سهبعدی با در اختیار داشتن بارهای خارجی اعمال شده به جسم (نیروهای حجمی و ترکشن سطحی)، قصد داریم جابجایی، کرنش و تنش خروجی که معادلات تعادل را ارضا می کند بدست آوریم. همانطور که از الاستیسیته به خاطر دارید، معادله تعادل جسم بهصورت زیر نوشته می شود:
از سوی دیگر شرایط مرزی حاکم بر یک مسئله در دو دسته کلی جابجایی و ترکشنهای سطحی جای میگیرد. در ادامه باید سعی کنیم تا به زبان ریاضی، مفاهیم شرایط مرزی را پیادهسازی کنیم.
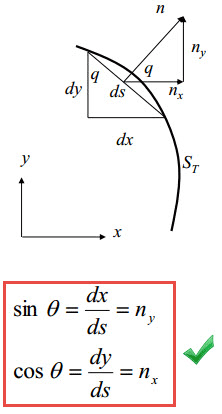
با تجزیه بردار ترکشن و استخراج مؤلفههای بردار نرمال، خواهیم داشت:
اگر معادلات تعادل را برای یک المان گوهای در راستای محور x در نظر بگیریم، داریم:
برای درک بهتر پارامترهای nx و ny به شکل زیر توجه کنید:
رابطه کرنش – جابجایی
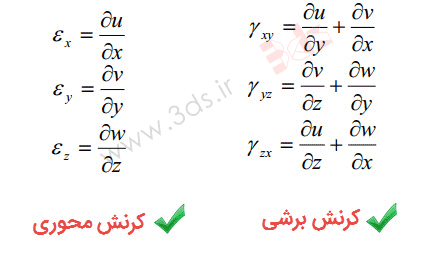
در خصوص مجموعه روابط کرنش – جابجایی به تفصیل در مجموعه پستهای پیشین بحث کردهایم و در این بخش تنها به ذکر روابط بسنده میکنیم:
رابطه تنش – کرنش
بدون شک همه شما با قانون هوک در الاستیسیته خطی آشنا هستید. چنانچه بخواهیم ماتریس الاستیسیته یا همان E را که در قانون هوک مورد استفاده قرار میگیرد در سه بعد استخراج کنیم، خواهیم داشت:
همچنین میدانهای جابجایی در این حالت عبارتند از:
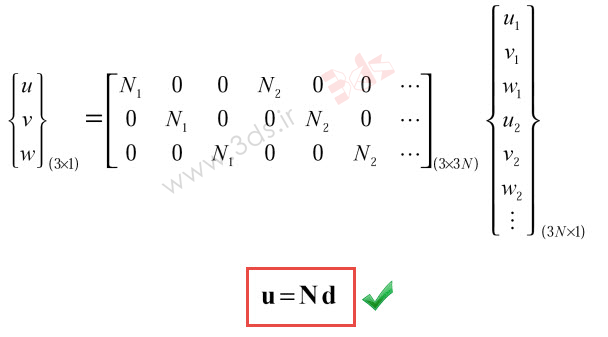
و یا در فرم ماتریسی:
با استفاده از روابط پیشین، قادر خواهیم بود تا بردار کرنش و ماتریس سختی را استخراج نماییم:
برای محاسبه انتگرال بالا، غالباً نیاز به استفاده از انتگرالگیری عددی خواهیم داشت. در ادامه مجموعه پستهای اجزا محدود، شما را با المانهای سهبعدی آشنا خواهیم کرد.
آموزشهای اجزا محدود ما را دنبال کنید و حرفهای بیاموزید . . .
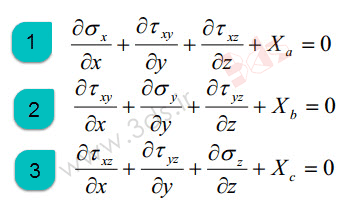
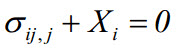




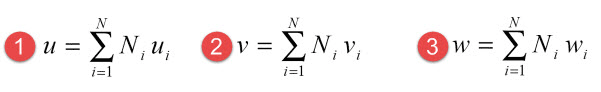


با سلام و تشکر از سایت بسیار مفیدتون و برای حسن خلقتون برای پاسخ گویی به سوال ها.
سوالی داشتم و اون این است که probabilisticدر اجزای محدود یعنی چه؟ آیا اطلاعاتی در این مورد دارید یا خیر
با تشکر
سلام
با همین کلیدواژه سرچ کنید منبع به تعداد کافی وجود داره