هدف آموزش: در ادامه سری آموزش آباکوس، در این آموزش شما با مسائل تنش صفحه ای، درک و شناخت مفهوم کرنش صفحه ای، تقارن در بار و هندسه مسئله، مسائل تقارن محوری، اصول حاکم بر مسئله تنش صفحه ای و کرنش صفحه ای و شناخت الزامات و شرایط لازم مسائل تقارن محوری آشنا خواهید شد.
ضرورت شناخت نوع مسئله پیش از تحلیل
پیشتر در باب اهمیت تشخیص نوع مسئله قبل از شروع تحلیل اجزاء محدود توضیحاتی ارائه کردیم. در آموزش حاضر شما را با سه مفهوم مهم و اساسی در سادهسازی تحلیل اجزای محدود معرفی میکنیم. این موضوع از این حیث حائز اهمیت است که کار شبیهسازی همواره با سادهسازیهای معقول و منطقی عجین شده است. در واقع تحلیلگر خبره شخصی است که بتواند پیش از شروع به شبیهسازی مسئله مورد نظر، فرضیات ساده کننده را بخوبی تشخیص دهد و با بکار بستن آنها بتواند حجم و هزینه محاسبات را کاهش دهد و در عین حال به نتایج دقیق و مطلوب دست یابد.
شناخت مسائل تنش صفحهای
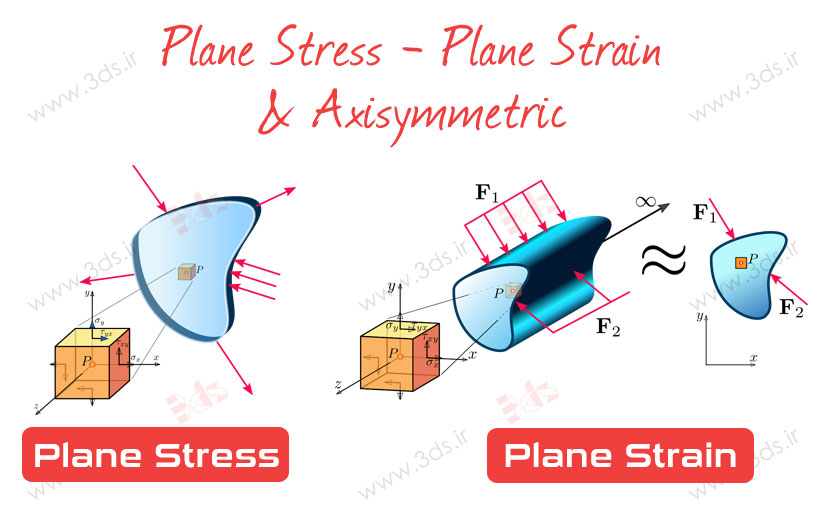
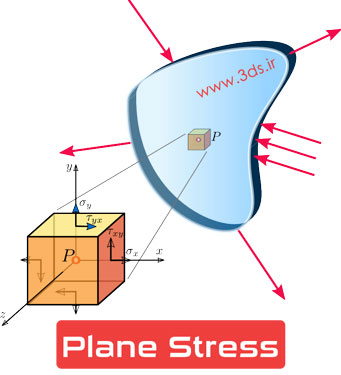
بدون شک شما نیز به این موضوع واقف هستید که در عمل، تمامی مسائل سه بعدی هستند و پدیدهای در دو بعد در دنیای اطراف ما وجود ندارد اما در شرایط خاص و برای حالتهایی از تنش و کرنش، میتوان مسائل جامدات را با سادهسازی از حالت سه بعدی به دوبعدی تبدیل نمود. در سازههای صفحهای با ضخامت کم و ثابت (ضخامت نسبت به بقیه ابعاد کمتر از 0.1 باشد) در صورتی که بارگذاری در همان صفحه xy صورت گیرد با یک مسئله تنش صفحهای مواجه هستیم. بهبیان دیگر در یک محیط پیوسته زمانی که بردار تنش در راستای یک صفحه خاص صفر باشد، حالت تنش صفحهای وجود دارد. مفهوم ریاضی این عبارت این است که مؤلفههای تنش عمودی و برشی با اندیس Z صفر است. تصویر زیر بیانگر یک مساله تنش صفحهای است.
کشش ورق تحت بارگذاریهای خوابیده و استوانه دو انتها باز تحت فشار داخلی نمونههای بارزی از حالت تنش صفحهای به شمار میروند.
مفهوم مسئله کرنش صفحهای
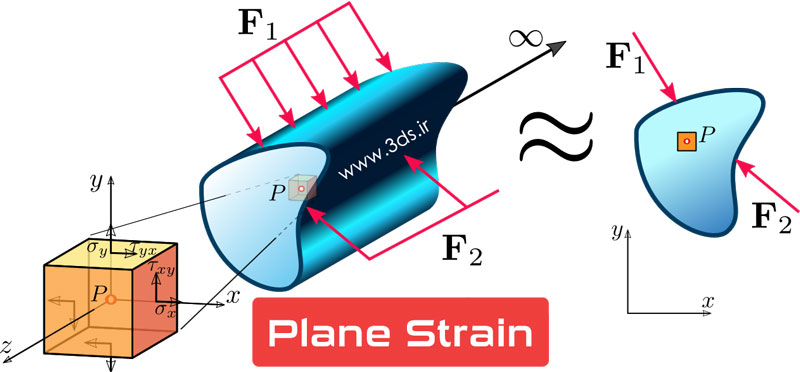
چنانچه ضخامت سازه زیاد و سطح مقطع آن یکنواخت باشد (سازه طویل) با فرض اعمال بار در راستای ضخامت، با یک مسئله کرنش صفحهای مواجه هستیم. به دیگر بیان، اگر ابعاد در یک راستا در مقایسه با سایر جهات بسیار بزرگ باشد، کرنش در راستای بلندترین طول، محدود بوده و میتواند صفر فرض شود. به بیان ریاضی، مؤلفههای تانسور کرنش با اندیس Z برابر صفر است. تصویر زیر بیانگر یک مساله کرنش صفحهای است.
در تحلیل کرنش صفحهای، علیرغم صفر بون کرنش در راستای Z، تنش در این راستا صفر نیست. میتوانید صحت این موضوع را به کمک روابط هوک بین تنش و کرنش بررسی نمایید. بدنه سد تحت بار فشاری آب و تغییر شکل قطعهای که در یک امتداد مانند ZZ مقید گردیده است (مثل نورد طولی ورق)، از برجستهترین نمونه های مسائل کرنش صفحهای به شمار میآید.
مفهوم تقارن محوری و اصول مدلسازی مسائل تقارن محوری
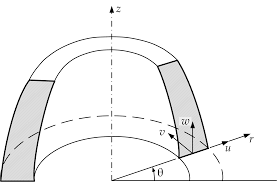
در حالتی که در هندسه و بارگذاری، تقارن وجود داشته باشد، مسئله از نوع متقارن محوری است. وجود هر دو شرط به شکل همزمان الزامی ست و عدم تأمین شرط هندسی و یا بارگذاری، مسئله را از حالت تقارن محوری خارج می کند. مخزن استوانه ای، مخروطی و کروی تحت فشارهای داخلی و یا خارجی و بسیاری از مخازن دیگ تحت فشار در زمره مسائل تقارن محوری هستند. بسیاری از فرآیندهای مکانیکی یا تغییر شکل را می توان تقارن محوری فرض نمود. به عنوان مثال، کشش یک میله استوانه ای، کشش سیم و بسیاری دیگر از فرآیندهای تغییر شکل را می توان به صورت تقارن محوری تحلیل نمود. به همین جهت، این نوع تحلیل در مسائل تنش از اهمیت و کاربرد زیاد برخوردار است.
نرمافزار Abaqus با هدف کاهش حجم محاسبات و صرفهجویی در زمان حل، دارای مدل و نیز المان متقارن محوری است. جسم متقارن به جسمی اطلاق میگردد که از دوران یک سطح حول محور تقارن ایجاد شود. خاصیت مدلسازی تقارن محوری این است که برای حل مسئله، تنها همین مولد جسم تقارن محوری شبکهبندی میشود و عملا نیازی به ایجاد شبکه اجزای محدود بر روی جسم سهبعدی نیست. در این حالت تنها کافیست سطح مقطعی را مدل کنید که از دوران آن حول محور تقارن میانی، مدل سهبعدی مورد نظر شما ایجاد شود (در اصطلاح، مولد شکل).
تذکر: در تاریخ 24 آبان 95 آموزشی تحت عنوان “المان تقارنمحوری” در سایت قرار گرفت.

سلام به همه
دوستان تو بعضی از مقالات مدل متقارن محوری میگیرن و بعدش خروجی توزیع ضخامت یا sth میگیرن در صورتی وقتی با اباکوس شبیه سازی میکنیم سکشن باید سالید گرفت که به طبع نمیشه اون خروجی گرفت.
ایا راه دیگه ای داره یا مدل 3d در نظر میگیرن و نتایج بدست میارن؟