اهداف آموزش: آشنایی با انتگرالگیری عددی، مزایای انتگرالگیری عددی، آشنایی با روش انتگرالگیری گاوس، مرتبه تابع مورد استفاده در روش گاوس، معرفی جدول توابع وزنی در انتگرالگیری عددی گاوس
همانگونه که پیشتر نیز اشاره شد روش اجزاء محدود یکی از روشهای عددی برای حل معادلات دیفرانسیل حاکم بر مسائل و پدیدههای فیزیکی است. در تحلیلهای عددی، انتگرالیری عددی شامل مجموعه الگوریتمها و دستورالعملهای گستردهای است که برای محاسبه مقدار عددی یک انتگرال معین و با تعمیم مفهوم و محتوای این تعریف در یافتن حل عددی معادلات دیفرانسیل بکار میرود. قصد داریم تا در این مبحث به اصول این روش حل عددی بپردازیم تا شما همراهان گرامی را کمی با پشتپرده حل مسائل در Abaqus و سایر نرمافزارهای حوزه اجزای محدود آشنا کنیم. قطعاً این آشنایی مقدماتی میتواند بعدها در شناخت مسائلی نظیر مفهوم المان، نوع المان و انتخاب حلگرهای ونیز به شکل کاملاً پیشرفته در مباحث برنامهنویسی رفتار مواد مختلف مفید واقع شود.
هدف انتگرالگیری عددی
مسئله اصلی در انتگرالگیری عددی، محاسبه حل تقریبی برای انتگرال معین (F(x روی بازه a تا b با درجه دقت قابل قبول است. چنانچه (F(x تابعی هموار بوده و دامنه انتگرالگیری نیز محدود باشد، روشهای بیشماری برای تقریب حاصل این انتگرال با دقت مورد نظر وجود دارد. دلایل مستحکمی در استفاده از روش انتگرالگیری عددی وجود دارد که دو مورد از مهمترین آنها به شرح زیر هستند:
- ممکن است فرمول برای تابع زیر انتگرال به شکل تحلیلی وجود داشته باشد اما گاهاً رسیدن به یک آنتیمشتق که از توابع مقدماتی بهره گیرد بسیار دشوار و یا غیرممکن است. منظور از آنتیمشتق در ریاضیات، همان یافتن تابع (F(x است که تابعی مشتقپذیر بوده و در حقیقت پاسخ انتگرال است. مثالی برای این موضوع تابع (F(x)=Exp (-x2 است که آنتیمشتق آن قابلیت نوشته شدن به شکل توابع مقدماتی را ندارد.
- ممکن است یافتن (F(x بهصورت سمبولیک امکانپذیر باشد اما گاهی تقریب عددی جواب بسیار سادهتر و سریعتر از یافتن تابع تحلیلی است. مثالی از این مورد حالتی است که (F(x به شکل یک سری نامتناهی ایجاد میشود.
همواره در حل مسائل مهندسی پارامتر زمان نقش تعیین کنندهای را ایفا میکند. بیگمان رسیدن به دقت قابل قبول در زمان معقول ایدهآلترین حالت ممکن در ذهن مهندسین است. لذا استفاده از انتگرالگیری عددی که در کنار سرعت بالای محاسبه، دقتهای بسیار قابل قبولی ارائه میدهد بسیار مورد توجه محققین قرار گرفته است.
آشنایی با انتگرالگیری عددی
توابع پیچیده را که به سهولت قابل انتگرالگیری نیستند، میتوان نخست با یک چند جملهای تقریب زده و سپس انتگرالگیری عددی نمود. اگر تابع به طور قابل توجهی از خطی بودن دور باشد، آنگاه خطای قابل ملاحظهای انتظار میرود. ولی این خطا را میتوان با افزایش تعداد تقسیمبندیها در فاصله X0 تا Xn کاهش داد. میتوان از چند جملهای های مرتبه بالاتر نیز برای تقریب زدن تابع استفاده نمود، بگونهای که دقت کار بالا برود. در این حالت صورت کلی انتگرال عبارتست از:
((I=∑ (wi f(Xi و i=0,…,n
که در آن n+1 تعداد نقاط نمونه است. در واقع بجای محاسبه انتگرال به شکل تحلیلی، مقدار تابع زیر انتگرال در نقاطی خاص در یک ضریب وزنی ضرب شده و حاصل مقادیر فوق در نقاط تعیین شده (تعداد نقاط بستگی به مرتبه تابع دارد) با یکدیگر جمع میشود و عدد حاصل جواب تقریبی انتگرال خواهد بود.wi چند جملهای ضریب وزنی بوده و در معادله فوق در صورت مساوی بودن فواصل نقاط نمونه، مقدار ثابت خواهند داشت. بر حسب انتخاب نقاط و ضرایب وزنی، روشهایی از قبیل قانون نقطه میانی، قانون ذوزنقهای، روش سیمپسون و . . . وجود دارد.
تعداد نقاط لازم برای انتگرالگیری و جدول ضرایب وزنی
اگر نامساوی بودن فواصل در انتخاب نقاط مجاز باشد و نقاط نیز به گونهای قرار گرفته باشند که بهترین تقریب چند جمله ای را بدهند، آنگاه برای تطابق دادن یک چند جملهای از مرتبه 2n-1 تعداد 2n متغیر خواهیم داشت. این روش کارایی قابل توجهی دارد و موسوم به تقریب گاوسی میباشد. به دیگر بیان در روش گاوس با انتخاب n نقطه (و محاسبه مقدار تابع زیر انتگرال در این نقاط و ضرب مقدار حاصل در ضریب وزنی آن نقطه) میتوان حداکثر یک تابع از مرتبه 2n-1 را با دقت مطلوب تقریب زد. به خاطر حفظ کلیت، مختصات نقاط نمونه یا گاوسی و ضرایب وزنی معمولا با حدود انتگرالگیری میان +1 و -1 تعریف میشوند.
مقادیر ضرایب وزنی کاملا مشخص و بر حسب تعداد نقاط، تعیین شدهاند و در جداول مرجع موجودند. در جدول زیر مقادیر ضرایب وزنی تا 4 نقطه انتگرالگیری گاوسی وجود دارد. به تقارن موجود در ضرایب وزنی توجه کنید.
| تعداد نقاط انتگرالگیری | ضرایب وزنی | حداکثر درجه تابع تحت پوشش |
|---|---|---|
| 2 | w1=1.00000000 w2=1.00000000 |
3 |
| 3 | w1=0.55555556 w2=0.88888889 w3=0.55555556 |
5 |
| 4 | w1=0.34785480 w2=0.65214520 w3=0.65214520 w4=0.34785480 |
7 |
اگر به این موضوع علاقمند ید و بدنبال یک مرجع مناسب هستید مطالعه کتاب “روشهای عددی پیشرفته تألیف دکتر غلامحسین مجذوبی، انتشارات دانشگاه بوعلی سینا” را به شما پیشنهاد میکنیم. دید مؤلف در نگارش کتاب سمت و سوی اجزا محدود نیز دارد و میتواند برای شما عزیزان مفید واقع شود.
منبع : آکادمی نرمافزارهای مکانیک
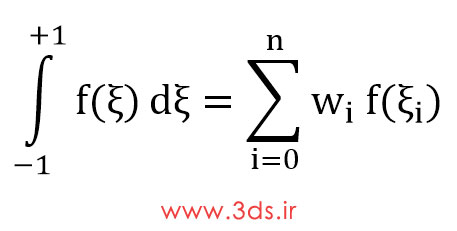

سلام
آیا در آباکوس میتوان تعیین کرد که انتگرال گیری با تعداد نقاط 2 باشد یا 3 یا 4 ؟؟؟
سلام
این موضوع به انتخاب المان برمیگرده
میتونید پست های مربوط به المانهای کاهش یافته و … را در بخش اجزای محدود سایت دنبال کنید
سلام مرسی از مقاله خوبتون. جدولتون همه اطلاعات لازم در مورد وزن و تعداد نقاط رو داده اما راجع به مقادیر نقاط توضیحی ندادید! نقاط مناسب رو چگونه باید انتخاب کرد؟
سلام
بله، حق با شماست
باید نقاط هم مشخص باشه
میتونید یک سرچ ساده در گوگل بفرمایید؛ مطلب به اندازه کافی وجود داره
https://en.wikipedia.org/wiki/Gaussian_quadrature