حتماً شما همراهان گرامی بهخاطر دارید که در مجموعه پستهای پیشین از بحث اجزاء محدود، به معرفی المانهای مربعی خطی و نحوه استخراج ماتریس سختی در این المانها پرداختیم (آشنایی با المان مربعی خطی). با هدف تکمیل آموزشها در این حوزه و در ادامه مجموعه آموزشهای FEM تصمیم گرفتیم شما عزیزان را با فرمولبندی و اصول حاکم بر المان مربعی خطی در دستگاه مختصات طبیعی آشنا کنیم. ما را در این آموزش اجزا محدود همراهی کنید.
یادآوری: آشنایی با مختصات طبیعی در اجزاء محدود
همانطور که پیشتر و در معرفی المانهای مثلثی خطی نیز اشاره کرده بودیم، پایه و اساس تعریف یک سیستم مختصات طبیعی بر هندسه المان استوار بوده و هدف اصلی در استفاده از این دستگاه مختصات، تعریف مکان هندسی نقاط داخل المان بر اساس مختصات و موقعیت گرههای آن المان است. در واقع میتوان استفاده از دستگاه مختصات طبیعی در محاسبات مربوط به یک المان مربعی خطی را به منزله یک نگاشت از فضای دلخواه به فضایی دانست که هر مختصاتی در آن به بازه -1 تا 1 محدود میشود. استفاده از این دستگاه مختصات موجب سهولت در انتگرالگیری عددی و در نتیجه افزایش سرعت حل مسئله میگردد.
توابع شکل المان مربعی خطی در دستگاه مختصات طبیعی
همانطور که پیشتر و در معرفی المان مثلثی خطی نیز اشاره کردیم، مختصات طبیعی یک نقطه از المان دلخواه به شکل زوج مرتب (ξ, η) تعریف میشود. با توجه به توضیحات فوق مبنی بر محدود بودن بازه مختصات بین صفر و یک خواهیم داشت:
مطابق اصول حاکم در روش اجزا محدود، جابجایی در گرههای المان بهصورت زیر قابل استخراج است:
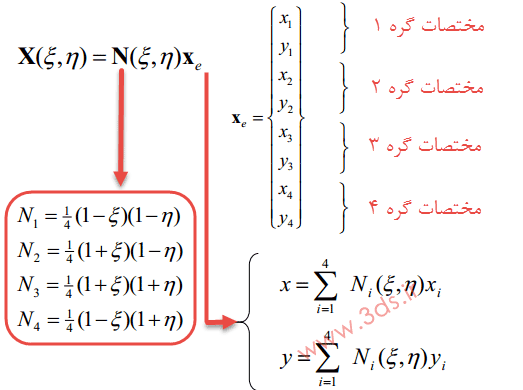
که در آن، Ni توابع شکل المان مربعی خطی در دستگاه مختصات طبیعی بوده و برابر با مقادیر زیر است:
بهعبارت دیگر؛
انتقال از دستگاه مختصات (x,y) به دستگاه مختصات طبیعی
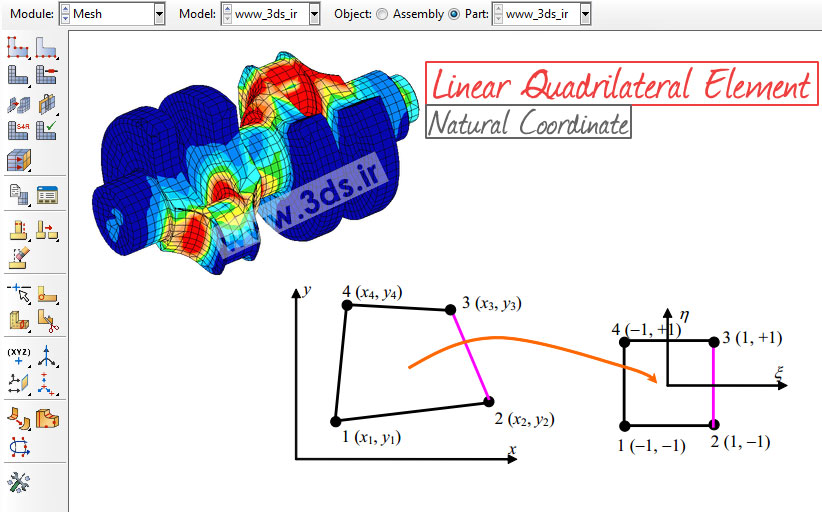
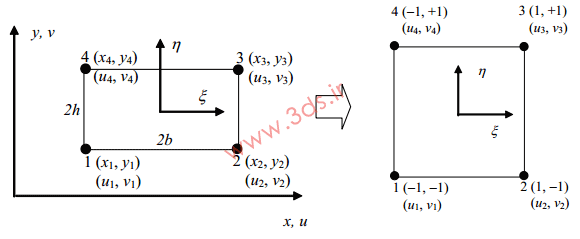
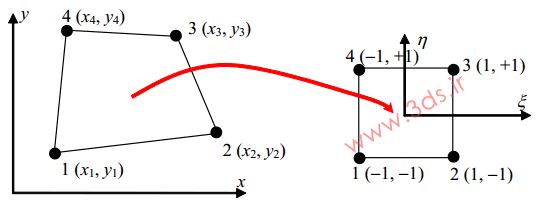
حال که با توابع شکل مربوط به المان مربعی خطی در سیستم مختصات طبیعی آشنا شدیم، قصد داریم تا اصول حاکم بر انتقال از دستگاه مختصات Global یا (x,y) به دستگاه مختصات طبیعی را مورد بررسی قرار دهیم. مطابق تصویر زیر، در نگاشت از مختصات اصلی به مختصات طبیعی داریم:
در نتیجه :
به دیگر بیان، برای نگاشت در مختصات هر گره داریم:
نکات مهم المان مربعی خطی
- توابع شکل که برای میانیابی مختصات در این المان استفاده میشوند با توابع شکل بکار گرفته شده در میانیابی میدان جابجایی مشابه هستند. بر همین اساس این المان، ایزوپارامتریک نامیده میشود.
- توجه داشته باشید توابع شکل استفاده شده در میانیابی مختصات و جابجایی لزوماً نباید یکسان باشند.
- استفاده از توابع شکل متفاوت در میانیابی مختصات و میدان جابجایی به ترتیب منجر به ایجاد المانهای سابپارامتریک (subparametric) و سوپرپارامتریک (superparametric) میشود.
در ادامه مباحث آموزشی اجزا محدود، به روش استخراج ماتریس سختی در المانهای ایزوپارامتریک خواهیم پرداخت.

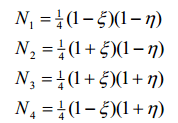
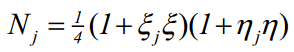
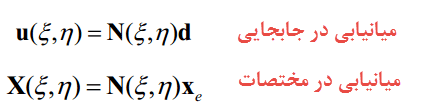

سلام مهندس
می خواستم به غیر از دستگاه مختصات کلی، یک دستگاه مختصات محلی هم تعریف کنم
ولی توو Job موقع حل ارور میده و میگه شرایط مرزی برای دو دستگاه مختصات تعریف شده
من با توجه به هندسه ی شکلم نیاز به چند دستگاه مختصات Local دارم
با احترام و ارادت
سلام
تعریف چند دستگاه مختصات مشکلی نداره؛ میتونید تعریف کنید و در انتهای حل جوابها را در هر دستگاهی که دوست داشتید مشاهده کنید
اما شما نمیتونید برای تعریف هر شرط مرزی از یک دستگاه مختصات استفاده کنید؛ تمامی شرطهای مرزی و بارگذاری باید بر اساس یک دستگاه مختصات باشه
موفق باشید . . .
سلام
میخواستم بدونم مفهومی داره که میدان تنش رو بر اساس مختصات کلی بررسی کنیم یا حتما باید مختصات محلی تعریف بشه ؟
سلام
مشکلی نداره
سلام وقت بخیر
یه ورق نازک انتخاب کردم و اونو با متلب و سپ و آباکوس مدل و آنالیز کردم . مسئله رو با تنش صفحه ایی برسی کردم .جالبه که نتایج سپ و متلب دقیقا یکیه ولی مال آباکوس اختلاف داره ؟؟؟؟ میشه راهنمایی کنین که ممکنه کجا اشتباه کرده باشم ؟
پارت آباکوس رو planer انتخاب کردم و shell . ابعاد 0.5×0.25 بارگذاری( 3000 -)درراستای افقی بروی المان سمت چپ
ضخامت ورق 0.025 و شرایط تکیه گاهی ، ضلع راست المان کلا مفصل u1=u2=0
مش بندی دو المان یعنی دومربع 0.25×0.25 با باندری کاندیشن و plane stress
نتایج متلب اومده 9.375 در جهت افقی و 1.97 در راستای عمودی عکس العمل تکیه گاهی
مال آباکوس اومده 9.375 در جهت افقی و 0.00701 در راستای عمودی عکس العمل تکیه گاهی
حسم میگه که دو حالت داره یا مش بندی اشتباهه و نحوه معادلات یا نوع مصالح که اولی احتمالش بیشتره ….
با تشکر ….
سلام
خب هر دو سناریویی که مطرح کردید را بررسی کنید
آباکوس یک ابزاره؛ ورودی غلط به شما خروجی غلط خواهد داد
سلام
اگر بخوایم xوy رو برای یک مثال عددی محاسبه کنیم چطوری میشه؟ میشه یه مثال بزنید؟ یرای ایکس وقتی N.x میکنم بجای زتا و اتا باید یم و منفی یک قرار بدیم در هر نقطه؟؟؟؟
سلام
شما یک تبدیل از فضای x و y به زتا و اتا دارید
معکوس این تبدیل براحتی در دسترس خواهد بود