اگر بهخاطر داشته باشید، در مجموعه پستهای پیشین به معرفی المان مثلثی خطی پرداختیم و با روش استخراج ماتریس سختی و توابع شکل آن آشنا شدیم. در ادامه بحثهای مربوط به این المان، تصمیم گرفتیم بنا بر قولی که به شما عزیزان داده بودیم، به معرفی مختصات طبیعی المان مثلثی خطی بپردازیم. پیشنهاد میکنم با ما در این آموزش اجزا محدود همراه باشید.
مختصات طبیعی چیست؟
به شکل خلاصه، تعریف یک سیستم مختصات طبیعی بر هندسه المان استوار است و مقدار آن بین صفر تا یک تغییر میکند. چنین سیستمهای مختصاتی دارای ویژگی خاصی هستند که بر اساس آن، یک مختصات خاص در یک گره از المان دارای مقدار یک بوده و در سایر گرههای موجود، برابر صفر است و تغییرات آن، بین گرهها بهصورت خطی است. از اینرو میتوانیم از سیستم مختصات طبیعی برای المانهای خطی دو گرهای، مثلثی سه نقطهای (خطی)، مربعی خطی (چهار نقطهای)، هرمی خطی و مشابه آن استفاده نماییم. هدف اصلی در استفاده از سیستم مختصات طبیعی، تعریف مکان یک نقطه داخل المان بر حسب مختصات متناسب با گرههای آن المان است.
مختصات طبیعی المان مثلثی خطی
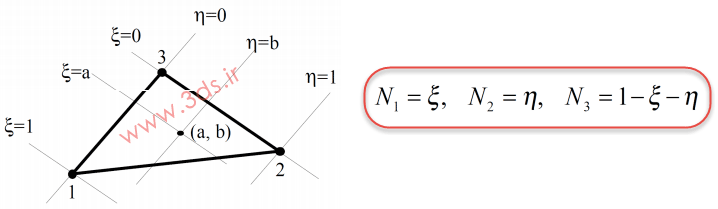
مختصات طبیعی یک نقطه از المان مثلثی را به صورت زوج مرتب (ξ, η) تعریف میکنند. لذا برای این دستگاه مختصات، میتوان توابع شکل را بهصورت زیر تعریف نمود (آشنایی با توابع شکل در اجزا محدود):
در این صورت، N1+N2+N3=1.
بهعبارت دیگر،
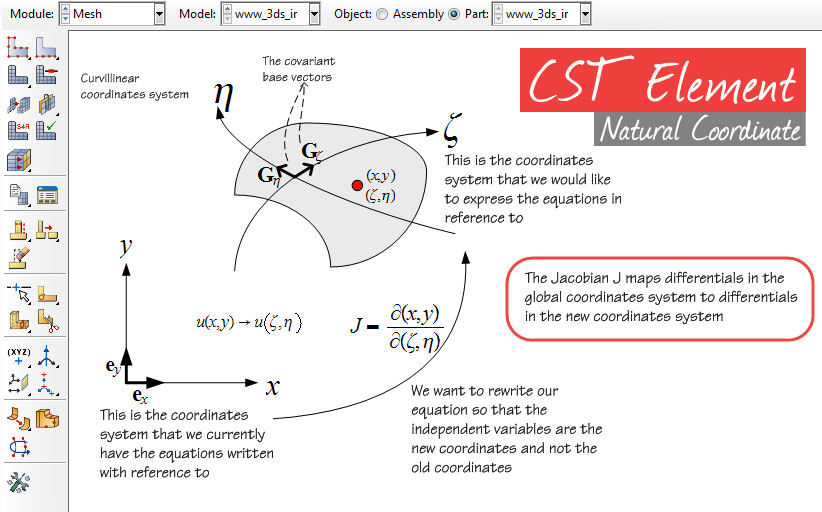
اگر دقت کرده باشید، دو دستگاه مختصات داریم؛ یکی مختصات طبیعی (ξ, η) که محلی است و دیگری، دستگاه مختصات سراسری (x,y). به کمک روابط زیر، میتوان دو دستگاه مختصات فوق را به یکدیگر مرتبط ساخت:
که در آن
xij = xi – xj , yij = yi – yj , (i,j=1,2,3)
در نتیجه، تغییر مکان (u,v) در داخل یک المان، بر حسب هر دو دستگاه مختصات فوق قابل بیان خواهد بود.
از سوی دیگر و بر اساس قاعده مشتق زنجیرهای داریم :
که در آن، J بهعنوان ژاکوبین ماتریس انتقال شناخته میشود و برابر است با:
با جایگذاری خواهیم داشت:
به صورت مشابه:
با استفاده از معادلات فوق و رابطه ε = Du = DNd = Bd میتوان ماتریس کرنش – تغییر مکان را بهدست آورد.
کاربردهای مهم المان مثلثی خطی
- استفاده برای سطوحی که دارای تغییرات کم کرنش هستند.
- استفاده برای سطوحی که دارای شبکه انتقالی (از شبکه ریز به شبکه درشت) است.
- قابل استفاده برای تخمین سریع و اولیه در مسائل دوبعدی
تذکر: از بکارگیری المانهای مثلثی خطی در سطوح دارای تمرکز تنش و یا سطوح بحرانی سازه نظیر اطراف سوراخها و گوشهها صرفنظر کنید.

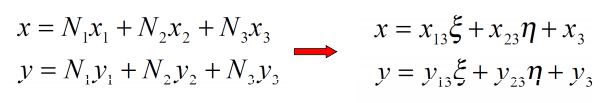
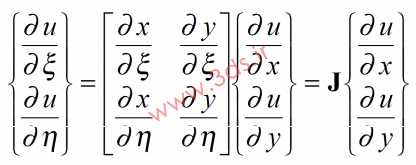
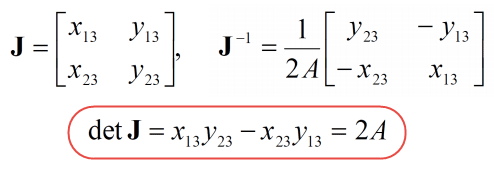
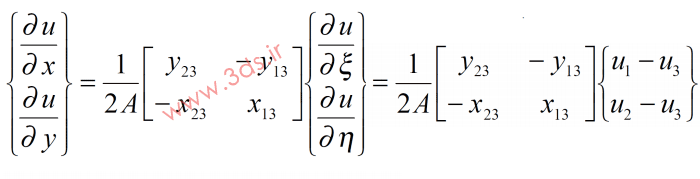
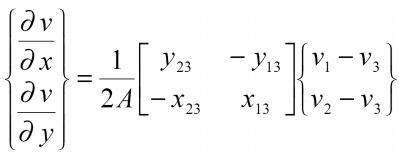


سلام
تغییر مختصات از کارتزین به قطبی چگونه انجام می شود؟
سلام
سؤالتون را دقیق طرح کنید
قصد تعریف دستگاه مختصات دارید یا نتایج را در دستگاه قطبی ببینید؟
نتایج را در دستگاه قطبی ببینم.
در ماژول visualization و از مسیر Tools > Coordinate system یک محور مختصات دلخواه ایجاد کنید
بعد از مسیر result > Options اقدام کنید؛ در پنجره باز شده به تب transformation وارد شوید و گزینه user-specified را انتخاب کنید
لیست محورهای مختصات ایجاد شده نشان داده شده و شما میتونید نتایج را در دستگاه مختصات دلخواه قرائت کنید