در پستهای پیشین از سلسه آموزشهای اجزا محدود، به ضرورت استفاده از این روش عددی در حل مسائل دوبعدی جامدات پرداختیم. همچنین المانهای مثلثی خطی را بهعنوان یکی از المانهای قابل استفاده در این مسائل برشمردیم و با اصول حاکم بر آن، توابع شکل و ماتریس سختی این المان آشنا شدیم. همچنین از مختصات طبیعی، بهعنوان یک مختصات محلی برای نگاشت المان در محدوده صفر تا یک نام بردیم و معادلات حاکم بر المان مثلثی خطی در مختصات طبیعی را مورد کنکاش قرار دادیم. قصد داریم تا در ادامه پستهای آموزش اجزا محدود، به معرفی المان مثلثی درجه دو بپردازیم. با ما در آموزش المانهای مثلثی درجه دو همراه باشید.
اصول حاکم بر المانهای مثلثی درجه 2
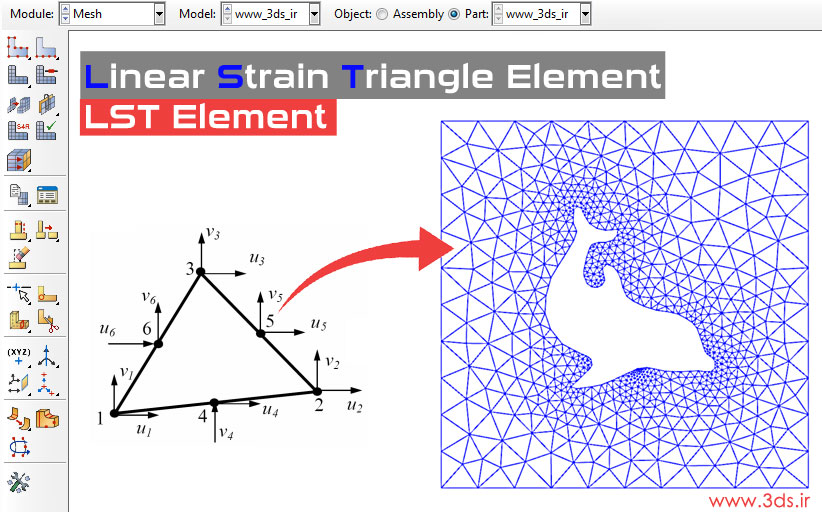
اگر بهخاطر داشته باشید، از المانهای مثلثی خطی با نام المانهای کرنش ثابت یاد کردیم و نشان دادیم که مقادیر تنش و کرنش در این المانها ثابت است و تغییر نمیکند. بر خلاف المانهای CST یا مثلثی کرنش ثابت، المانهای مثلثی درجه دو میدان کرنش خطی دارند، از اینرو LST یا Linear Strain Triangle Element نامیده میشوند.
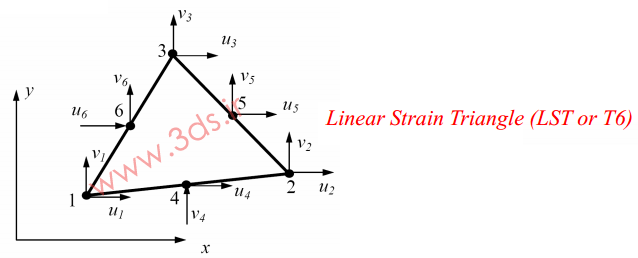
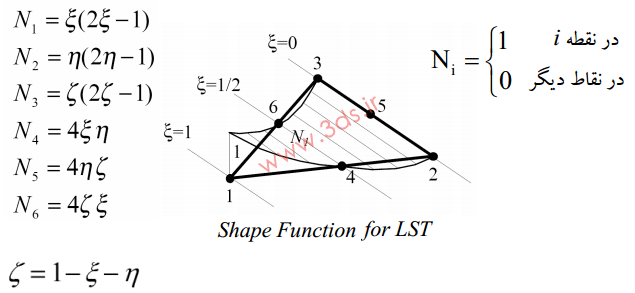
مطابق شکل فوق، در المان مثلثی درجه دو، شش گره (سه گره در رئوس المان و سه گره در وسط هر ضلع) وجود دارد که در جهت خلاف عقربههای ساعت شمارهگذاری میشوند. مشابه المانهای CST، در اینجا نیز هر گره دارای دو درجه آزادی (جابجایی در جهت x و y) است.
روابط حاکم بر المان مثلثی درجه دو
تغییر مکان داخل المانهای LST بهصورت توابع درجه دو بر حسب x و y در نظر گرفته میشود:
که در آن bi اعداد ثابتی هستند. با توجه به رابطه فوق و با یادآوری مباحث پایه اجزا محدود، میتوان نتیجه گرفت که مقادیر کرنش المان مثلثی مرتبه دوم، خطی بوده و در مقایسه با المان مثلثی خطی نتایج بهتری مورد انتظار است.
توابع شکل المان مثلثی درجه دو (LST) در مختصات طبیعی به شکل زیر خواهد بود:
همینطور، تغییر مکان در گرهها عبارت است از:
و ماتریس سختی المان مثلثی درجه دو (LST) از رابطه زیر قابل محاسبه خواهد بود:
اما در اینجا، BTEB تابعی مرتبه دو بر حسب x و y خواهد بود و در حالت کلی، انتگرال فوق باید با روشهای عددی محاسبه شود.
برتری المان مثلثی مرتبه دو (LST) نسبت به المان مثلثی خطی (CST)
- همانطورکه در قبل اشاره شد، مقادیر کرنش المان مثلثی مرتبه دو، خطی بوده و در مقایسه با المان مثلثی خطی که مقادیر کرنش ثابتی دارد، نتایج بهتری مورد انتظار است.
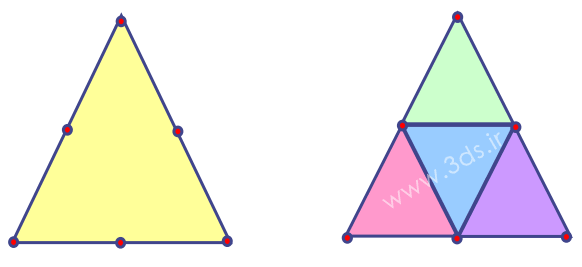
- همانطور که در شکل زیر نیز مشاهده میکنید هر المان مثلثی درجه 2 میتواند با چهار المان مثلثی خطی جایگزین شود (هر دو شکل چپ و راست دارای 6 گره و 12 درجه آزادی هستند). از اینرو میتوان گفت استفاده از المانهای مثلثی درجه دو سبب کاهش تعداد شبکه و زمان حل مسئله میگردد.
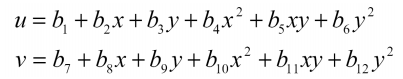
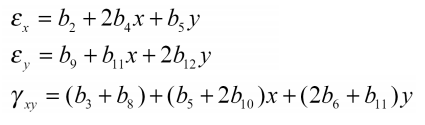
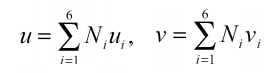
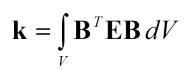

سلام خسته نباشید، یه سوال درمورد جزع مثلثی LST با ۱۲ گره (روی هر ضلع ۵گره) دارم ، اینکه برای نوشتن تابع شکل چطوری باید عبارت انتخاب کنیم برحسب کسی۱ کسی۲ و کسی۳؟؟
میشه از مثلث خیام پاسکال استفاده کرد؟ ممنون میشم اگه برای یک گره تابع شکل رو بنویسید ک باقی گره ها رو مطابق اون بدست بیارم،
خیلی سپاسگزارم.
سلام
بله؛ از مثلث پاسکال استفاده کنید (قواعدش مشخصه، با یه سرچ ساده هم میتونید پیدا کنید؛ یک چند جمله ای کامل با ضرایب نامعینه که شما باید با استفاده از قواعد حاکم بر توابع شکل (یک بودن در همان گره و صفر بودن در تمامی نقاط دیگر) این ضرایب را پیدا کنید در خصوص مسئله شما 15 ضریب نامعین برای هر نود وجود داره)
سلام وقت بخیر، آیا میشه LST رو در آباکوس مدل کرد ؟
فرق روشش با حالتی که CST داریم، چیه؟
سلام
https://www.quora.com/What-is-the-difference-between-CST-and-LST-in-finite-element-methods