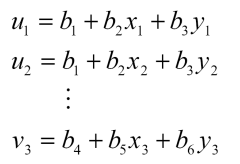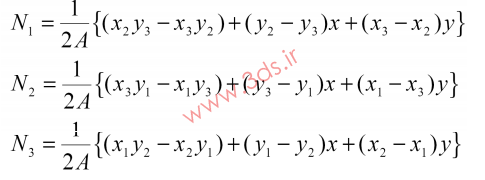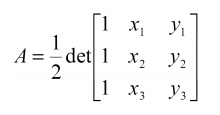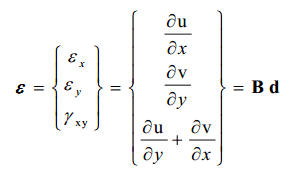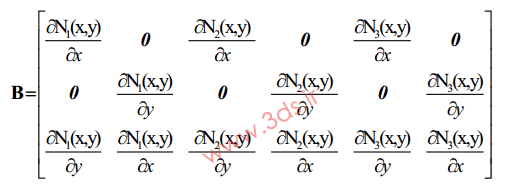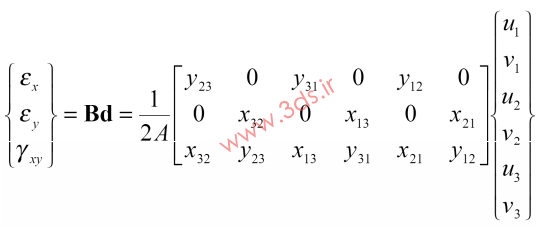پیش از این و در آموزشی جداگانه از سلسله مباحث آموزش اجزای محدود، به ضرورت بکارگیری اجزای محدود در مسائل دوبعدی تحلیل سازه و اصول حاکم بر این دسته از مسائل پرداختیم. چنانچه بخاطر داشته باشید، المانهای مثلثی خطی – درجه دو و المانهای مربعی خطی – درجه دو را بهعنوان المانهای مورد استفاده در مسائل دوبعدی معرفی کردیم و به شما همراهان گرامی قول دادیم در ادامه آموزشهای اجزا محدود، به معرفی المانهای مثلثی خطی بپردازیم. از اینرو تصمیم گرفتیم در این آموزش اجزاء محدود، به شکل تخصصی المانهای مثلثی خطی را مورد بررسی قرار دهیم و اصول حاکم، نحوه شمارهگذاری، روش استخراج ماتریس سختی، توابع شکل و میدان تنش را مرور نماییم. ما را در مسیر آموزش المانهای مثلثی خطی همراهی کنید.
اصول اولیه المان مثلثی خطی
بحث معرفی المانهای مثلثی خطی را با معرفی شکل ظاهری این المانها آغاز میکنیم.
همانطور که ملاحظه میکنید، در رئوس این المان سه گره وجود دارد که در جهت خلاف عقربههای ساعت شمارهگذاری میشوند. هر گره دارای دو درجه آزادی (جابجایی در دو جهت x و y) است و تغییر مکان در داخل المان به صورت توابع خطی در نظر گرفته میشود:
که در آن bi اعداد ثابتی هستند.
با داشتن میدان تغییر مکان فوق، مقادیر کرنش عبارتند از:
که مقادیر ثابتی برای کل المان خواهد بود. از اینرو، المان مثلثی خطی، المان مثلثی کرنش ثابت (CST – Constant Strain Triangle Element) نیز نامیده میشود.
معادلات حاکم بر المان مثلثی خطی
با توجه به اینکه در هر یک از گرههای المان مثلثی دو درجه آزادی از جنس تغییر مکان وجود دارد، میتوان معادلات تغییر مکان در گرههای این المان را بهصورت زیر نوشت:
حل شش معادله فوق منجر به یافتن مقادیر bi بر حسب تغییر مکان و مختصات گرهها خواهد شد. با جایگزینی مقادیر bi در رابطه اول (تغییر مکان داخل المان) خواهیم داشت:
که در این رابطه، توابع شکل به صورت توابعی خطی از مختصات عبارتند از:
که در آن
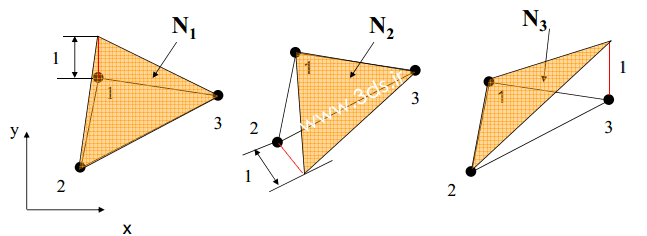
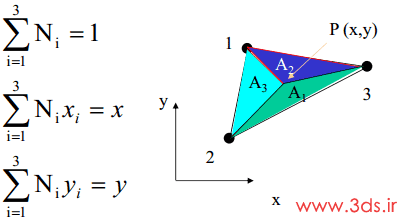
در واقع، توابع شکل المانهای مثلثی خصوصیاتی مانند شکل زیر از خود نشان میدهند:
بعبارت دیگر، مقدار تابع شکل Ni در گره iام برابر یک و در سایر گرهها برابر صفر خواهد بود. در واقع، برای هر نقطه از المان:
با مرور روابط پایه مکانیک، مقادیر کرنش بهصورت زیر خواهد بود:
که در آن،
لذا، مقادیر کرنش بر اساس روابط فوق به صورت زیر بدست خواهد آمد:
که در آن، xij = xi – xj و yij = yi – yj و همچنین i , j = 1, 2 , 3 است. از آنجایی که کرنشها برای کل المان مقادیر ثابتی هستند، مقدار تنش نیز (از رابطه تنش – کرنش) ثابت خواهد بود.
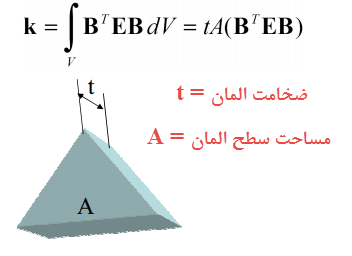
ماتریس سختی المان مثلثی
با توجه به روابط ذکر شده در پستهای آموزشی پیشین، ماتریس سختی المان مثلثی خطی مطابق رابطه زیر استخراج خواهد شد:
که یک ماتریس 6*6 متقارن خواهد بود.
در خصوص بکارگیری مختصات طبیعی برای المان مثلثی خطی در پستهای آموزشی بعدی صحبت خواهیم کرد.
لذت آموزش اجزا محدود را از دست ندهید …