اگر مجموعه مطالب آموزش اجزاء محدود سایت را دنبال کرده باشید، میدانید که در آموزشهای پیشین به معرفی مفاهیم پایه اجزاء محدود در مسائل دو بعدی و ضرورت بکارگیری روش اجزاء محدود در مسائل دو بعدی پرداختیم. همچنین با هدف آشنایی شما همراهان گرامی با روش اجزاء محدود در حل مسائل دو بعدی به معرفی المانهای مثلثی خطی، المان مثلثی درجه دو و نحوه استخراج ماتریس سختی در این المانها پرداختیم. امروز و در این پست از آموزش اجزاء محدود قصد داریم تا به معرفی المان مربعی خطی بپردازیم، با ویژگیها و روابط حاکم بر این المانها آشنا شویم و نحوه استخراج ماتریس سختی در المان مربعی خطی در دستگاه مختصات (x,y) را فراگیریم. با ما در این آموزش اجزاء محدود همراه باشید.
ویژگیهای المان مربعی خطی
همانطور که در المانهای مثلثی خطی اشاره کردیم، به دلیل فرمولبندی و روابط حاکم بر این المانها کرنش بدست آمده از FEM در هر المان مقدار ثابتی دارد. اما در المانهای مربعی خطی ماتریس کرنش، ثابت نیست و از اینرو میتوان گفت المانهای مربعی خطی نمایش دقیقتری از میدان تنش و کرنش در اختیار تحلیلگر قرار میدهند. همچنین بهدلیل شکل هندسی منظم و قاعدهمند این دسته از المانها، روابط حاکم بر آن از سهولت بیشتری برخوردار است.
روابط حاکم بر المان مربعی خطی
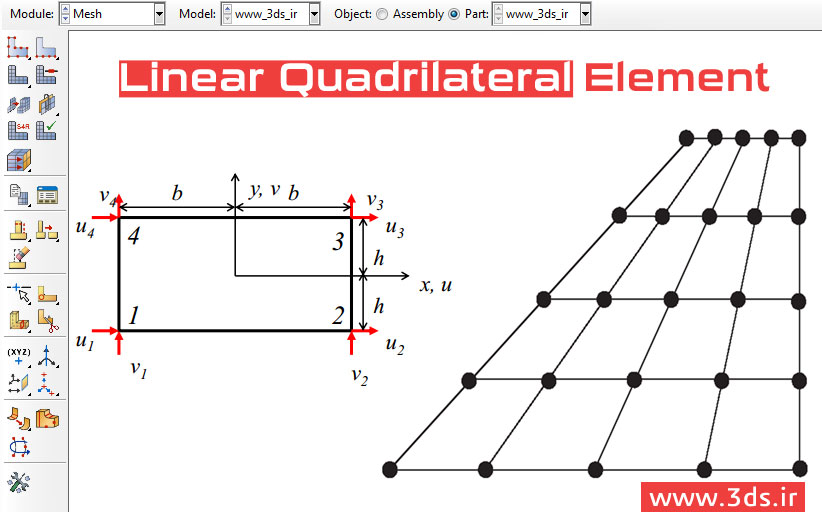
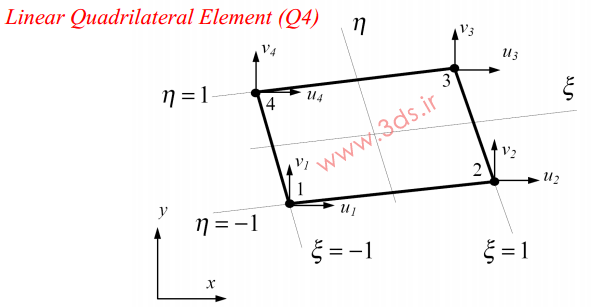
در ابتدای معرفی المان مربعی خطی توجه شما همراهان عزیز را به شکل ظاهری این المان جلب میکنیم.
همانطور که ملاحظه میکنید، المان مربعی خطی چهار گره در رئوس خود دارد که همانند المانهای مثلثی خطی در خلاف جهت عقربههای ساعت شمارهگذاری میشوند. هر گره دارای دو درجه آزادی (جابجایی در دو جهت x و y) است و تغییر مکان در داخل المان به صورت توابع زیر در نظر گرفته میشود:
که ai در این روابط اعداد ثابتی هستند.
حال با توجه به اینکه در هر یک از گرههای المان مربعی خطی دو درجه آزادی از جنس تغییر مکان وجود دارد، میتوان معادلات تغییر مکان در گرههای این المان را نوشته و با حل هشت معادله بدست آمده به شکل همزمان، مقادیر ai مربوطه را استخراج کرد. با جایگزینی مقادیر ai در رابطه مربوط به تغییر مکان داخلی المان، خواهیم داشت:
که در این رابطه، تابع شکل المان مربعی خطی بهصورت توابعی از مختصات عبارتند از:
ماتریس سختی المان مربعی خطی در دستگاه مختصات (x,y)
حال با توجه به مفاهیم پایه روش اجزاء محدود، ماتریس کرنش المان مربعی خطی بهصورت زیر قابل استخراج خواهد بود:
در این رابطه، B ماتریس کرنش – جابجایی بوده و از رابطه زیر بدست میآید:
در نهایت، ماتریس سختی المان مربعی خطی از رابطه زیر بدست خواهد آمد:
همانگونه که در المان مثلثی به معرفی مختصات طبیعی و روابط حاکم در این دستگاه مختصات پرداختیم؛ در ادامه مباحث آموزش اجزاء محدود به معرفی روش استخراج ماتریس سختی المانهای مربعی خطی در مختصات طبیعی خواهیم پرداخت.
استوار در سرزمین اجزاء محدود گام بردارید . . .

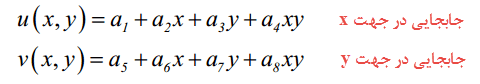
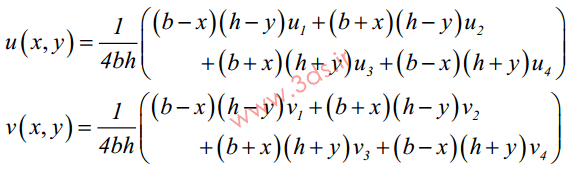
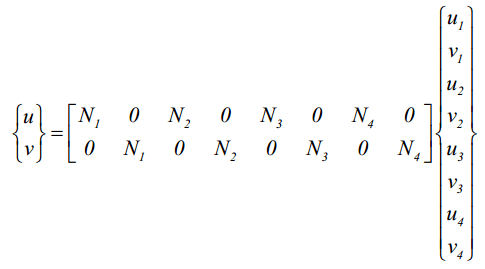
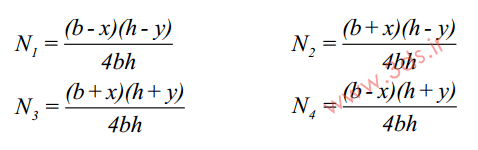
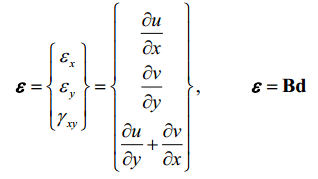
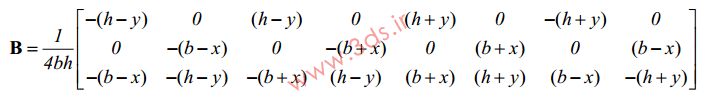
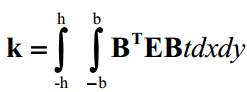

سلام
سوالی داشتم در مورد تنش حرارتی
اگر یک ورق داشته باشم و مرکزشو رو به اندازه یک دایره کوچیک حرارت بدم پس از ی مدتی باید کل ورق دماش به دمای مرکز برسه و تنش درش صفر بشه
میخواستم بپرسم چطور باید این موضوع رو در اباکوس مدل کنم.
ممنون
سلام
چندین مثال انتقال حرارت در سایت موجوده؛ لطفاً قبل از طرح سؤال سرچ کنید
در ضمن سؤالتون را در پست مرتبط بپرسید؛ مثال انتقال حرارت به اندازه کافی در سایت هست، شما در بحث اجزای محدود سؤالتون را مطرح میکنید