پیش از این و در مجموعه آموزشهای اجزا محدود، به تفصیل پیرامون المانهای مربعی خطی اطلاعاتی کسب کردیم. همچنین فرمولبندی این المانها در دستگاه مختصات طبیعی را آموختیم (المان مربعی خطی: دستگاه مختصات طبیعی). اگر بخاطر داشته باشید، در بررسی و یادآوری نکات مهم المان مربعی خطی، عنوان کردیم در صورتیکه توابع شکل بکار گرفته شده برای میانیابی میدان جابجایی با توابع شکل مورد نظر در میانیابی مختصات این المان مشابه باشد، المان مذکور را ایزوپارامتریک مینامیم. حال با توجه به اهمیت موضوع و جهت تکمیل سلسله آموزشهای اجزا محدود سایت، تصمیم گرفتیم به معرفی روش استخراج ماتریس سختی در المانهای ایزوپارامتریک بپردازیم. پیشنهاد میکنم با دقت این آموزش اجزا محدود را دنبال کنید.
فرمولبندی و میدان جابجایی و کرنش در المان ایزوپارامتریک
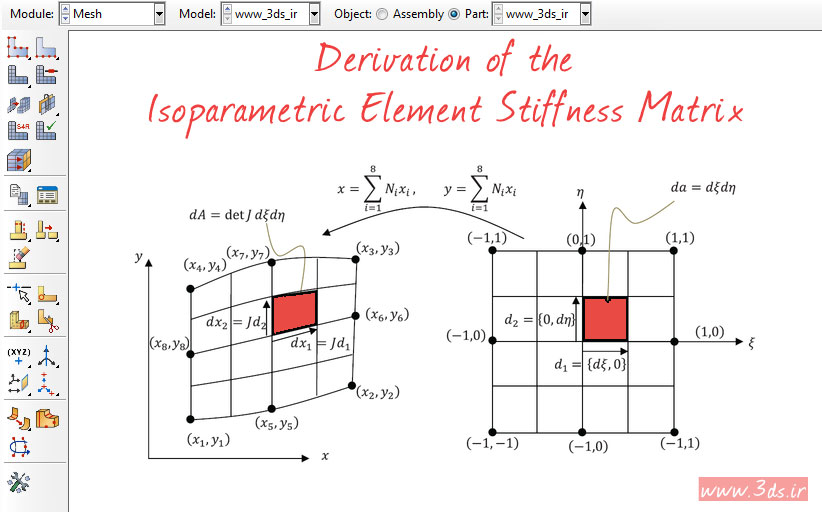
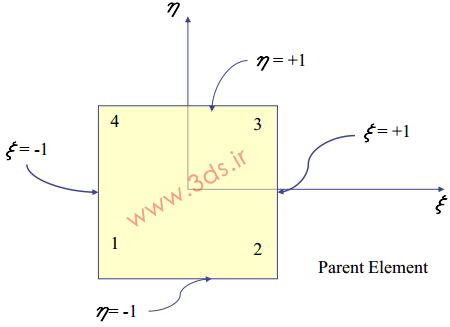
مطابق تصویر زیر، یک المان مربعی خطی در دستگاه مختصات طبیعی را در نظر بگیرید:
بر اساس اصول حاکم بر روش اجزا محدود در المانهای خطی میتوانیم مختصات هر نقطه از المان مورد نظر را به کمک مجموعه روابط زیر تعیین نماییم.
به بیان دیگر:
که در آن Ni بیانگر توابع میانیاب المان مربعی خطی در دستگاه مختصات طبیعی است. اگر به تعریف ارائه شده از المان ایزوپارامتریک دقت کنید انتظار داریم تا میدان جابجایی مورد نظر برای این المان نیز به کمک توابع میانیاب مشابه استخراج شود. به عبارت بهتر، میدان جابجایی در المان ایزوپارامتریک بر اساس توابع میانیاب مختصات، بدست آمده و مطابق رابطه زیر خواهد بود:
بدون شک شما همراهان گرامی میدانید که برای یافتن میدان کرنش باید از مشتقات میدان جابجایی المان بهره جست؛ لذا:
و یا در فرم ماتریسی:
از آنجایی که انتقال دستگاه مختصات به شکل منحصر بفرد و وارونپذیر است داریم:
بر اساس قانون مشتق زنجیرهای در توابع:
مطابق اصول پیشین، ماتریس ژاکوبین عبارت است از:
در نتیجه، میدان کرنش در المان ایزوپارامتریک از رابطه زیر استخراج خواهد شد:
به عبارت دیگر:
که در این رابطه:
همچنین، توابع میانیاب معرفی شده در این رابطه، به شکل زیر قابل محاسبه خواهند بود:
ماتریس سختی المان ایزوپارامتریک
حال که با اصول حاکم بر المان ایزوپارامتریک و استخراج میدان کرنش در این المان آشنا شدهایم، میتوانیم ماتریس سختی مربوط به المان ایزوپارامتریک را نیز بدست آوریم. از اینرو:
و مطابق اصول انتقال
در نتیجه:
فراموش نکنید در استخراج ماتریس سختی المان ایزوپارامتریک نیز از اصول انتگرالگیری عددی گاوس استفاده خواهیم کرد.
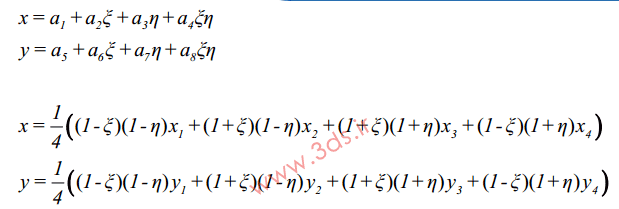
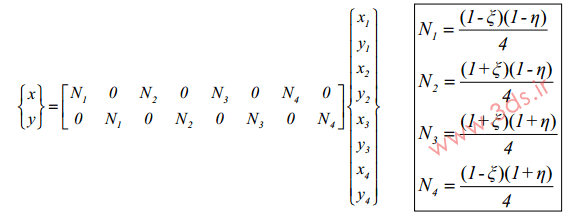
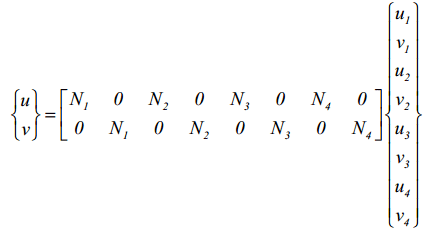
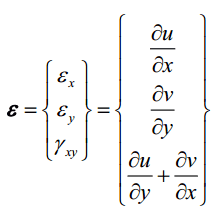
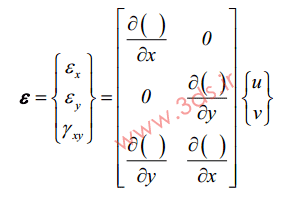

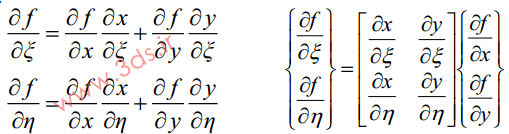
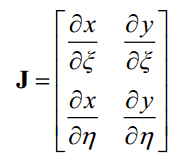
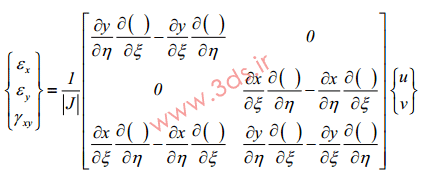
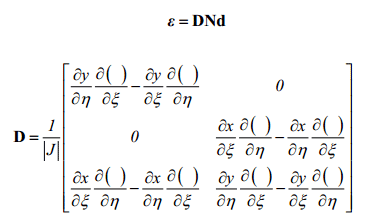
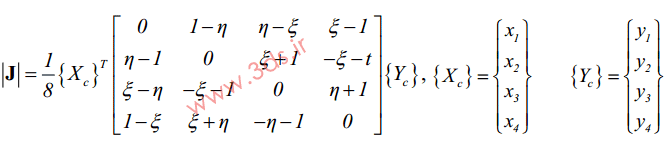
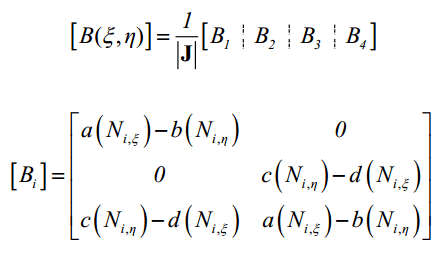
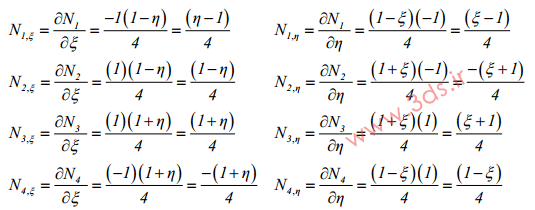
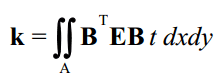
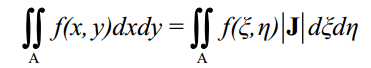
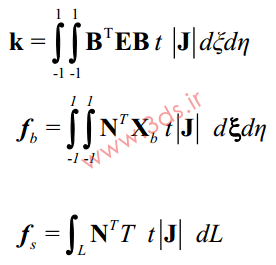
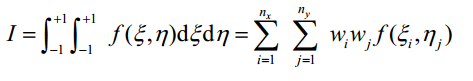

سلام، وقت بخیر
من در حل مسئله اعمال بار متمرکز در یکی از گره های المان ایزوپارامتریک چهار گره های خطی با هشدار زیر روبرو میشم:
THE SYSTEM MATRIX HAS 1 NEGATIVE EIGENVALUES.
مسئله بدون خطا کامپلیت میشه ولی در ماژول visualization هیچ خروجی نمایش داده نمی شود و پیغام زیر نمایش داده می شه:
“Abaqus Deformation and/or analytical surface extent is too large as compared with the model”
ممنون میشم در خصوص علت بروز هشدار و پیغام بالا راهنمایی بفرمائید.
سلام
برخورد نداشتم متأسفانه