شرایط مرزی در مسائل سازه

اگر مجموعه مطالب آموزشی اجزای محدود را دنبال کرده باشید به خوبی از اهمیت اعمال شرایط مرزی به شکل صحیح و شناخت کامل آن آگاهید. پیشتر و در پستی جداگانه شرایط مرزی ضروری و طبیعی در اجزای محدود را به شما معرفی کردیم. قصد داریم تا در این بخش، به آموزش انواع شرایط مرزی متداول در تحلیل مسائل سازه بپردازیم. به شما پیشنهاد می‌کنیم این آموزش کاربردی را از دست ندهید.

1. ممانعت از حرکت جسم صلب یا Rigid Body Motion در قطعه

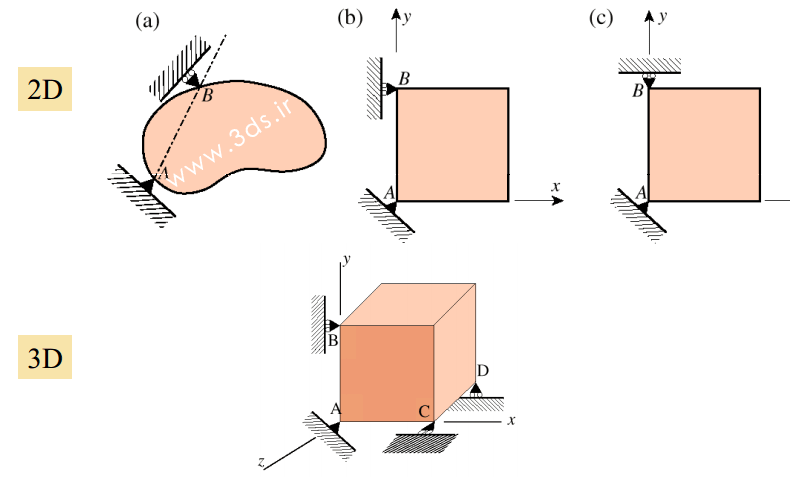
شاید یکی از ابتدایی‌ترین شرایط مرزی ضروری برای یک تحلیل، ممانعت از حرکت جسم صلب یا Rigid Body Motion در قطعه مورد نظر باشد. مود جسم صلب به حالتی اطلاق می‌شود که هیچ‌گونه انرژی در جسم ذخیره نشود. شکل زیر، شرایط مرزی مانع از وقوع این پدیده را در مسائل دو و سه‌بعدی نشان می‌دهد.

2. شرط تقارن

یکی دیگر از شرایط مرزی متداول در تحلیل، شرط تقارن است. زمانی که اجزای سازه به شکل متناوب و یا قرینه قرار گرفته باشند، اصطلاحا مسئله را متقارن می‌نامیم. انواع تقارن از دیدگاه اجزای محدود در چند گروه عمده زیر خلاصه می‌شوند:

• تقارن آینه‌ای (یا در اصطلاح انعکاسی)
• تقارن سیکلی (دورانی)
• تقارن محوری (axisymmetric)
• تقارن انتقالی (تکرار شونده)

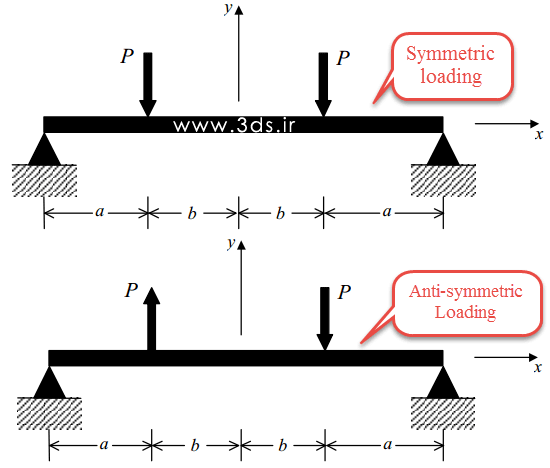
ذکر این نکته ضروریست که در تحلیل‌های ارتعاشی و کمانش سازه، به شکل کلی اصول تقارن نباید در حل اجزای محدود لحاظ شوند زیرا سازه‌های متقارن غالبا مودهای ارتعاشی و کمانشی پادمتقارن از خود نشان می‌دهند. بعلاوه توجه داشته باشید که سازه می‌تواند از نقطه نظر هندسی دارای تقارن و از منظر بارگذاری پاد‌متقارن باشد. تصویر زیر به‌خوبی این موضوع را نشان می‌دهد.

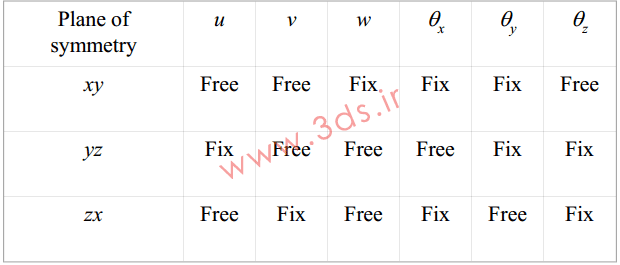
جدول زیر نیز نشان می‌دهد که شرط مرزی تقارن در حالت‌های مختلف، کدامیک از درجات آزادی را تحت تأثیر قرار می‌دهد.

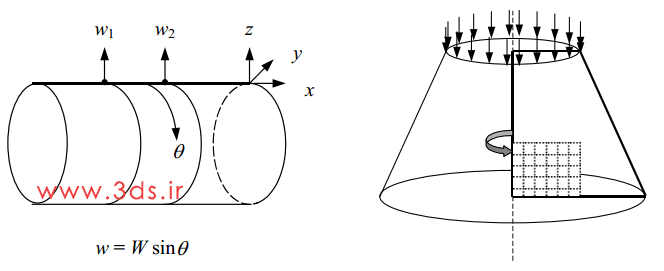
اگر بحث مقایسه مسائل تنش / کرنش صفحه ای و تقارن محوری را مطالعه کرده باشید، می‌دانید که تقارن همزمان در بارگذاری و هندسه، مسئله را متقارن محوری خواهد کرد. یادآوری این نکته خالی از لطف نیست که عدم برقراری هر یک از شروط فوق، مسئله را از تقارن محوری خارج می‌نماید. بزرگ‌ترین مزیت استفاده از قید تقارن محوری، کاهش چشمگیر هزینه و زمان حل مسئله بدلیل استفاده از المان‌های یک و دو‌بعدی است. در مدل‌سازی این دسته از مسائل تنها کافیست مولد جسم (که هندسه سه‌بعدی مسئله از دوران آن حول محور تقارن ایجاد می‌شود) را شبکه‌بندی کنید و بوسیله این تکنیک حجم محاسبات خود را به نحو قابل‌توجهی کاهش دهید. همان‌گونه که در شکل زیر می‌بینید، تقارن در بار و هندسه موجب شده است تا پوسته استوانه‌ای (سمت چپ) و سازه سه‌بعدی (مخروط ناقص سمت راست) را به کمک المان‌های ساده یک و دو‌بعدی مدل‌سازی نماییم.

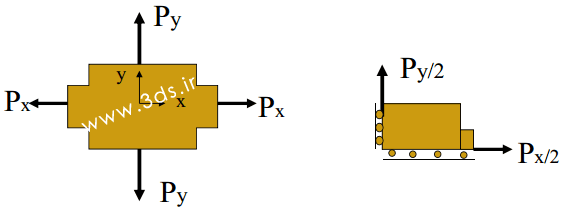
بدون شک، تسلط بر موارد فوق می‌تواند در کاهش حجم محاسبات و صرفه‌جویی در زمان بسیار مؤثر باشد. بعنوان مثال بدلیل وجود تقارن انعکاسی در ورق سمت چپ، استفاده از مدل یک‌چهارم و اعمال صحیح شرایط مرزی به آن، هزینه حل مسئله را به شکل قابل‌توجهی کاهش خواهد داد.

شعار اصلی حل اجزای محدود را فراموش نکنید: ! Keep it simple

منبع : آکادمی نرم‌افزارهای مکانیک