اهداف آموزش: با مطالعه این آموزش، مجموعه‌ای از تکنیک‌های بسیار کاربردی در مدل‌سازی اجزا محدود مسائل مختلف را فرا خواهید گرفت. همچنین قادر خواهید بود از شبکه اجزا محدود با سایز مناسب در مسئله خود استفاده کنید، شرایط مرزی مناسب را بر مسئله خود اعمال کنید و با تکنیک‌هایی کاربردی هزینه محاسباتی و زمان حل مسئله خود را مدیریت کنید.
در روش اجزاء محدود (روش المان محدود – Finite Element Method) از توابع پیوسته چند تکه‌ای و هموار برای تقریب کمیت مجهول مورد نظر سود برده می‌شود. هدف اصلی در این روش، یافتن حل یک مسأله پیچیده از طریق جایگزینی آن با یک مدل ساده‌تر است. در این مجموعه آموزش‌هایی مرتبط با روش اجزاء محدود درج خواهد شد. این آموزش‌ها شامل مباحث مقدماتی و پیشرفته جهت آشنایی شما با پشت پرده حل مساله در نرم‌افزارهای تحلیل و شبیه‌سازی مانند آباکوس (ABAQUS) و انسیس (ANSYS) و LS-DYNA و … خواهد بود. این آموزش ها مقدمه ای بر آموزش آباکوس است.
اهداف آموزش: در این آموزش با اصول اجزا محدود حاکم بر حل یک مسئله آشنا خواهید شد. همچنین با معرفی و شناخت توابع شکل، پل میان محاسبات گره‌ای و محاسبات داخل المان را برقرار خواهیم کرد. شناخت الزامات و چارچوب‌های توابع شکل در اجزا محدود از دیگر اهدافی است که با مطالعه این آموزش به آن خواهید رسید.
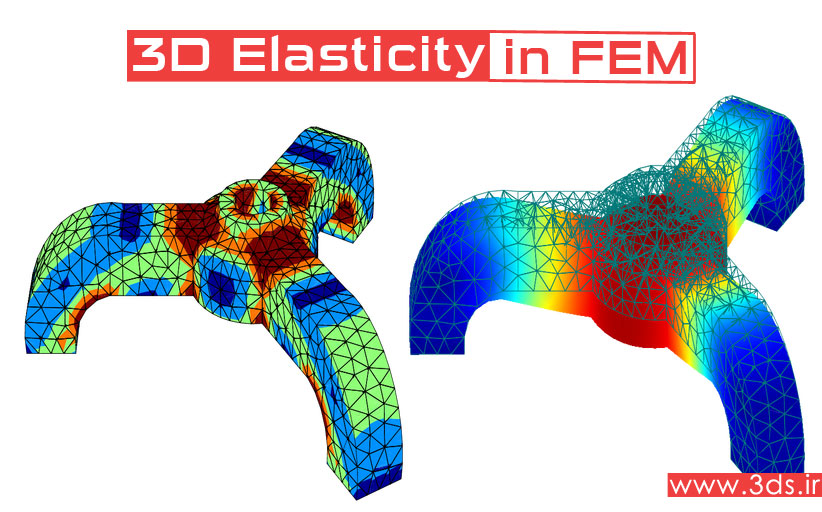
اهداف آموزش: در این آموزش شما با مفاهیم الاستیسیته سه‌بعدی، نحوه پیاده‌سازی الاستیسیته سه‌بعدی در اجزا محدود، معادلات تعادل در الاستیسیته، استخراج روابط کرنش – جابجایی و نهایتا نحوه استخراج روابط تنش – کرنش در الاستیسیته آشنا خواهید شد.
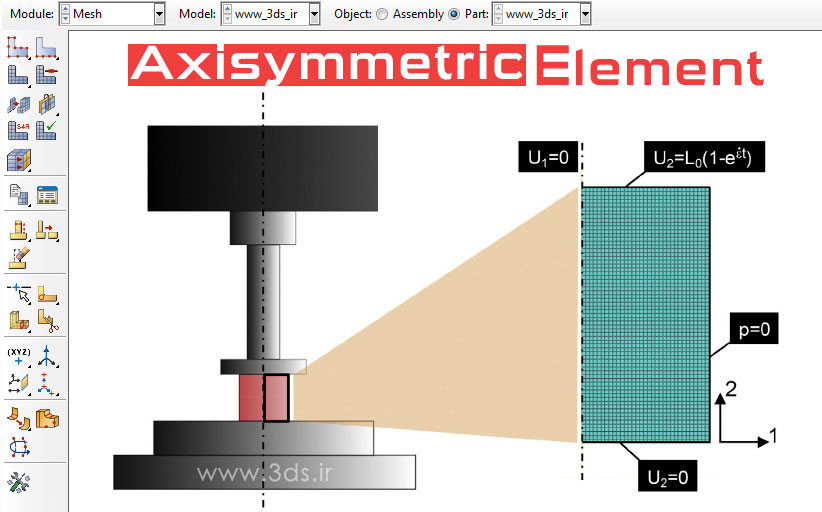
هدف آموزش: در این آموزش شما با المان تقارن محوری، اصول حاکم بر المان تقارن محوری، مفهوم تقارن محوری در اجزاء محدود، مثال‌های متنوع از تقارن محوری آشنا خواهید شد.
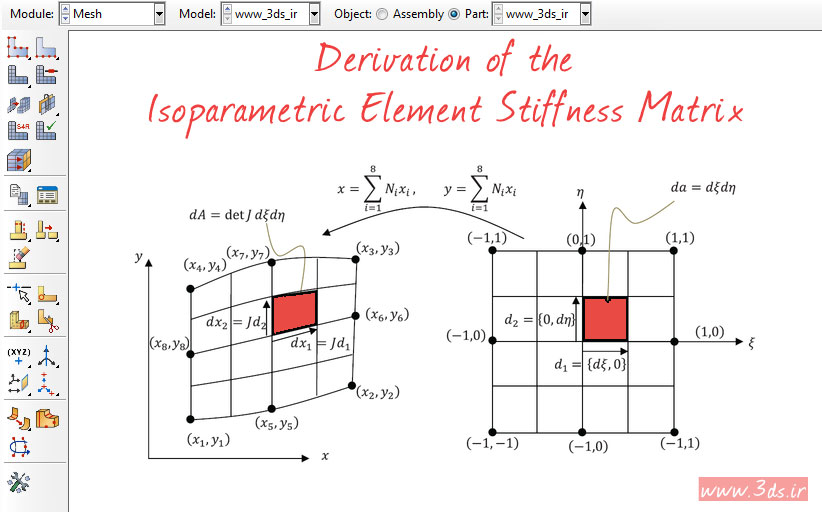
پیش از این و در مجموعه آموزش‌های اجزا محدود، به تفصیل پیرامون المان‌های مربعی خطی اطلاعاتی کسب کردیم. همچنین فرمول‌بندی این المان‌ها در دستگاه مختصات طبیعی را آموختیم (المان مربعی خطی: دستگاه مختصات طبیعی). اگر بخاطر داشته باشید، در بررسی و یادآوری نکات مهم المان مربعی خطی، عنوان کردیم در صورتی‌که توابع شکل بکار گرفته شده برای میانیابی میدان جابجایی با توابع شکل مورد نظر در میانیابی مختصات این المان مشابه باشد، المان مذکور را ایزوپارامتریک می‌نامیم. حال با توجه به اهمیت موضوع و جهت تکمیل سلسله آموزش‌های اجزا محدود سایت، تصمیم گرفتیم به معرفی روش استخراج ماتریس سختی در المان‌های ایزوپارامتریک بپردازیم. پیشنهاد می‌کنم با دقت این آموزش اجزا محدود را دنبال کنید.
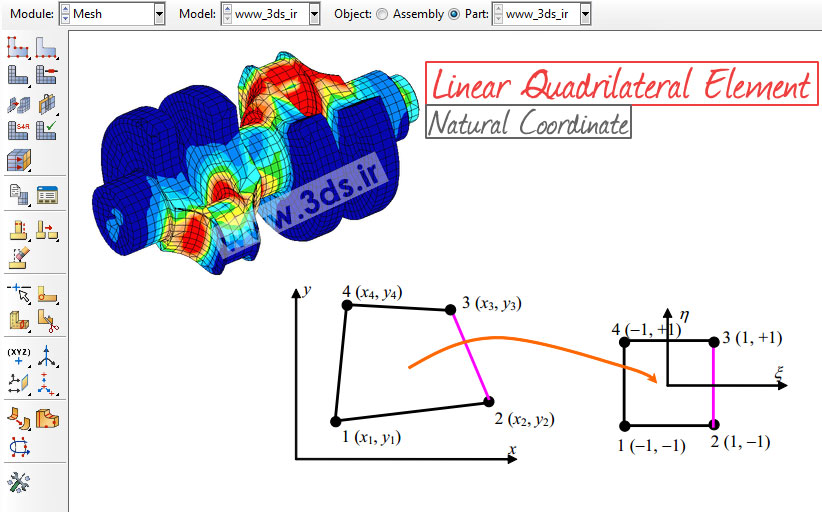
حتماً شما همراهان گرامی به‌خاطر دارید که در مجموعه پست‌های پیشین از بحث اجزاء محدود، به معرفی المان‌های مربعی خطی و نحوه استخراج ماتریس سختی در این المان‌ها پرداختیم (آشنایی با المان مربعی خطی). با هدف تکمیل آموزش‌ها در این حوزه و در ادامه مجموعه آموزش‌های FEM تصمیم گرفتیم شما عزیزان را با فرمول‌بندی و اصول حاکم بر المان مربعی خطی در دستگاه مختصات طبیعی آشنا کنیم. ما را در این آموزش اجزا محدود همراهی کنید.
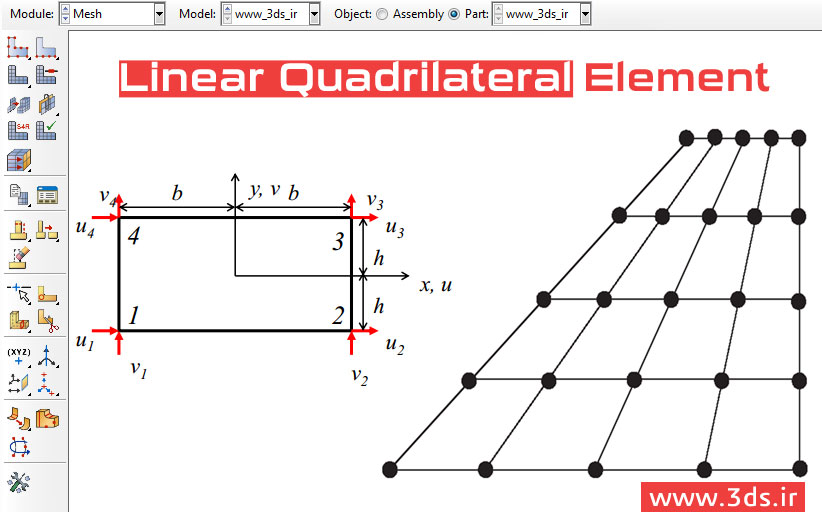
اگر مجموعه مطالب آموزش اجزاء محدود سایت را دنبال کرده باشید، میدانید که در آموزش‌های پیشین به معرفی مفاهیم پایه اجزاء محدود در مسائل دو بعدی و ضرورت بکارگیری روش اجزاء محدود در مسائل دو بعدی پرداختیم. همچنین با هدف آشنایی شما همراهان گرامی با روش اجزاء محدود در حل مسائل دو بعدی به معرفی المان‌های مثلثی خطی، المان مثلثی درجه دو و نحوه استخراج ماتریس سختی در این المان‌ها پرداختیم. امروز و در این پست از آموزش اجزاء محدود قصد داریم تا به معرفی المان مربعی خطی بپردازیم، با ویژگیها و روابط حاکم بر این المان‌ها آشنا شویم و نحوه استخراج ماتریس سختی در المان مربعی خطی در دستگاه مختصات (x,y) را فراگیریم. با ما در این آموزش اجزاء محدود همراه باشید.
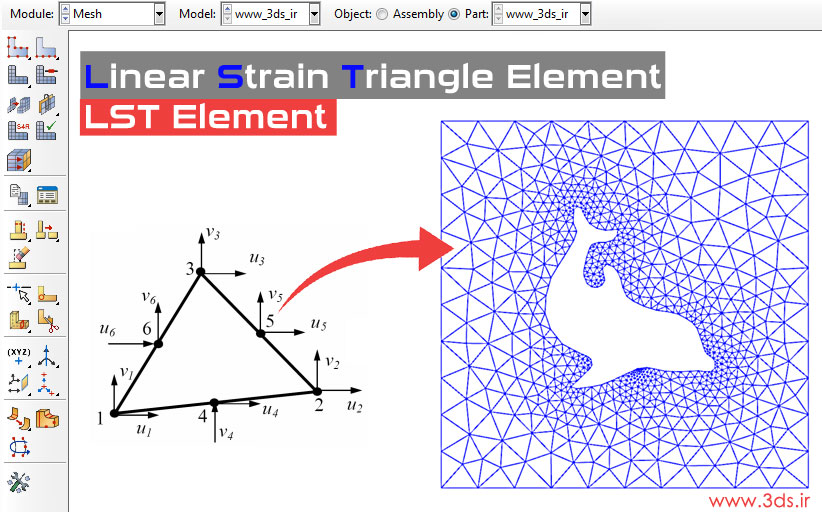
در پست‌های پیشین از سلسه آموزش‌های اجزا محدود، به ضرورت استفاده از این روش عددی در حل مسائل دوبعدی جامدات پرداختیم. همچنین المان‌های مثلثی خطی را به‌عنوان یکی از المان‌های قابل استفاده در این مسائل برشمردیم و با اصول حاکم بر آن، توابع شکل و ماتریس سختی این المان آشنا شدیم. همچنین از مختصات طبیعی، به‌عنوان یک مختصات محلی برای نگاشت المان در محدوده صفر تا یک نام بردیم و معادلات حاکم بر المان مثلثی خطی در مختصات طبیعی را مورد کنکاش قرار دادیم. قصد داریم تا در ادامه پست‌های آموزش اجزا محدود، به معرفی المان مثلثی درجه دو بپردازیم. با ما در آموزش المان‌های مثلثی درجه دو همراه باشید.
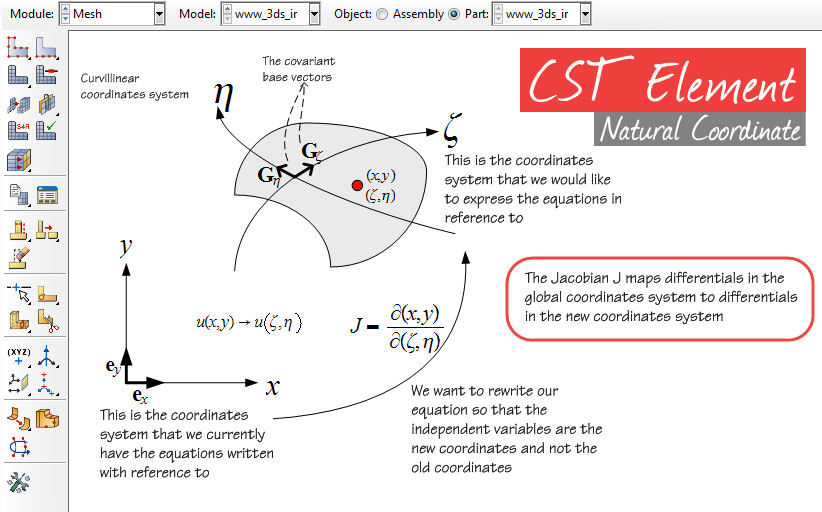
اگر به‌خاطر داشته باشید، در مجموعه پست‌های پیشین به معرفی المان مثلثی خطی پرداختیم و با روش استخراج ماتریس سختی و توابع شکل آن آشنا شدیم. در ادامه بحث‌های مربوط به این المان، تصمیم گرفتیم بنا بر قولی که به شما عزیزان داده بودیم، به معرفی مختصات طبیعی المان مثلثی خطی بپردازیم. پیشنهاد می‌کنم با ما در این آموزش اجزا محدود همراه باشید.
پیش از این و در آموزشی جداگانه از سلسله مباحث آموزش اجزای محدود، به ضرورت بکارگیری اجزای محدود در مسائل دوبعدی تحلیل سازه و اصول حاکم بر این دسته از مسائل پرداختیم. چنانچه بخاطر داشته باشید، المان‌های مثلثی خطی - درجه دو و المان‌های مربعی خطی - درجه دو را به‌عنوان المان‌های مورد استفاده در مسائل دوبعدی معرفی کردیم و به شما همراهان گرامی قول دادیم در ادامه آموزش‌های اجزا محدود، به معرفی المان‌های مثلثی خطی بپردازیم. از این‌رو تصمیم گرفتیم در این آموزش اجزاء محدود، به شکل تخصصی المان‌های مثلثی خطی را مورد بررسی قرار دهیم و اصول حاکم، نحوه شماره‌گذاری، روش استخراج ماتریس سختی، توابع شکل و میدان تنش را مرور نماییم. ما را در مسیر آموزش المان‌های مثلثی خطی همراهی کنید.